题目内容
16.在等差数列{an}中,an=3n-31,记bn=|an|,则数列{bn}的前30项和755.分析 设等差数列{an}的前n项和为Sn,当n≤10时,Tn=-Sn,当n>10时,Tn=Sn-2S7.
解答 解:在等差数列{an}中,an=3n-31,
∴a1=-28,a2=-25,d=3,a10=-1,a11=2,bn=|an|,
数列{bn}的前30项和T30=28+25+22+…+1+2+5+…+59
=$\frac{1+28}{2}×10$+$\frac{2+59}{2}×20$
=755.
故答案为:755.
点评 本题考查数列的各项的绝对值的前n项和的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
7.函数$f(x)=\sqrt{{x^0}-x}$的定义域是( )
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,0)∪(0,1) | D. | (-∞,0)∪(0,1] |
8.下列命题中正确的是( )
| A. | 若?服从正态分布N(1,2),且P(?>2)=0.1,则P(0<?<2)=0.2 | |
| B. | 命题:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
5.已知数列{an}前n项和满足Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$ (n≥2),a1=1,则an=( )
| A. | n | B. | 2n-1 | C. | n2 | D. | 2n2-1 |
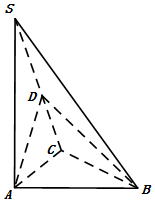 如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC
如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC