题目内容
11.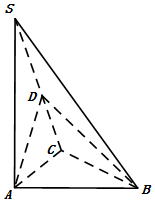 如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC
如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC(Ⅰ)求证:AB⊥平面SAC
(Ⅱ)若SA=2AB=3AC,求二面角S-BD-A的余弦值.
分析 (Ⅰ)在平面SAC中,过点S作SH⊥AD,垂足为H,由面面垂直的性质可得AB⊥SH,再由SA⊥平面ABC,得AB⊥SA,结合线面垂直的判定可得AB⊥平面SAC;
(Ⅱ)不妨设AC=2,AB=3,AS=6,由(Ⅰ)知,AB⊥平面SAC,得AB⊥AC,分别以AB、AC、AS所在直线为z、y、z轴建立空间直角坐标系.求出两个平面平面ABD与平面SBD的一个法向量,由法向量所成角的余弦值可得二面角S-BD-A的余弦值.
解答 (Ⅰ)证明:如图,在平面SAC中,过点S作SH⊥AD,垂足为H,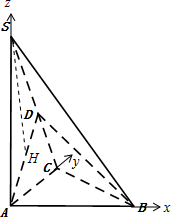
∵平面ABD⊥平面SAC,平面ABD∩平面SAC=AD,
∴SH⊥平面ABD,∴AB⊥SH.
又SA⊥平面ABC,∴AB⊥SA.
∵SA∩SH=S,∴AB⊥平面SAC;
(Ⅱ)解:不妨设AC=2,AB=3,AS=6,
由(Ⅰ)知,AB⊥平面SAC,∴AB⊥AC,
分别以AB、AC、AS所在直线为z、y、z轴建立空间直角坐标系.
则有A(0,0,0),B(3,0,0),C(0,2,0),S(0,0,6),D(0,1,3).
设平面ABD的一个法向量$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$,则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{AB}=3{x}_{1}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{AD}={y}_{1}+3{z}_{1}=0}\end{array}\right.$,
取z1=1,得$\overrightarrow{{n}_{1}}=(0,-3,1)$.
同理可得平面SBD的一个法向量$\overrightarrow{{n}_{2}}=(-2,-3,-1)$.
∴cos<$\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}$>=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{8}{\sqrt{10}×\sqrt{14}}=\frac{4\sqrt{35}}{35}$.
∴二面角S-BD-A的余弦值为-$\frac{4\sqrt{35}}{35}$.
点评 本题考查直线与平面垂直的判定,训练了利用空间向量求二面角的平面角,是中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $-\frac{{\sqrt{2}}}{5}$ | B. | $\frac{{\sqrt{2}}}{5}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
| A. | $\frac{{{e^2}+1}}{2}$ | B. | $\frac{{{e^2}-3}}{2}$ | C. | $\frac{{{e^2}+3}}{2}$ | D. | $\frac{{{e^2}-5}}{2}$ |
| A. | $\frac{3}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |