题目内容
7.函数$f(x)=\sqrt{{x^0}-x}$的定义域是( )| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,0)∪(0,1) | D. | (-∞,0)∪(0,1] |
分析 由0指数幂的底数不为0,根式内部的代数式大于等于0联立不等式组求解.
解答 解:由$\left\{{\begin{array}{l}{x≠0}\\{1-x≥0}\end{array}}\right.$,解得x≤1且x≠0,
∴函数$f(x)=\sqrt{{x^0}-x}$的定义域是(-∞,0)∪(0,1].
故选:D.
点评 本题考查函数的定义域及其求法,是基础的计算题.

练习册系列答案
相关题目
17.曲线y=tanx在点($\frac{π}{4}$,1)处的切线的斜率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | 2 |
18.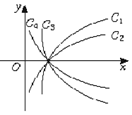 图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )
图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )
 图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )
图中曲线是对数函数y=logax的图象,已知a取$\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$四个值,则相应于C1,C2,C3,C4的a值依次为( )| A. | $\frac{4}{3}$,$\sqrt{3}$,$\frac{3}{5}$,$\frac{1}{10}$ | B. | $\sqrt{3}$,$\frac{4}{3}$,$\frac{1}{10}$,$\frac{3}{5}$ | C. | $\sqrt{3}$,$\frac{4}{3}$,$\frac{3}{5}$,$\frac{1}{10}$ | D. | $\frac{4}{3}$,$\sqrt{3}$,$\frac{1}{10}$,$\frac{3}{5}$ |
12.已知3x+x3=100,[x]表示不超过x的最大整数,则[x]=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
17.“因为指数函数y=ax(a>0且a≠1)是增函数,而y=($\frac{1}{3}$)x是指数函数,所以y=($\frac{1}{3}$)x是增函数.”在上面的推理中( )
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提、小前提及推理形式都错误 |
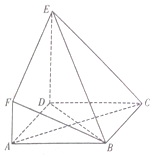 如图,四边形ABCD是正方形,DE⊥平面ABCD,AF∥DE,AF=$\frac{1}{2}AD=\frac{1}{3}$ED=1.
如图,四边形ABCD是正方形,DE⊥平面ABCD,AF∥DE,AF=$\frac{1}{2}AD=\frac{1}{3}$ED=1.