题目内容
6．（1）画出函数y=|x-2|的图象，写出函数的增区间和减区间；（2）已知A={x|-2＜x＜-1或x＞1}，B={x|a≤x＜b}，A∪B={x|x＞-2}，A∩B={x|1＜x＜3}，求实数a，b的值．
分析 （1）由题意画出函数图象，利用图象写出单调区间；
（2）根据两个集合的运算a，b的范围或者具体数值即可．
解答 解：
（1）
函数的减区间为（-∞，2]，增区间为（2，+∞）．
（2）因为A∩B={x|1＜x＜3}，
所以b=3，-1≤a≤1．
因为A∪B={x|x＞-2}，
所以-2＜a≤-1．
所以a=-1．
综上可知a=-1，b=3．
点评 本题（1）考查了函数的图象以及单调性；（2）考查集合的运算．比较基础．
练习册系列答案
阅读快车系列答案
相关题目
17．曲线y=tanx在点（$\frac{π}{4}$，1）处的切线的斜率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | 1 | D． | 2 |
18．
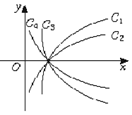图中曲线是对数函数y=logax的图象，已知a取$\sqrt{3}$，$\frac{4}{3}$，$\frac{3}{5}$，$\frac{1}{10}$四个值，则相应于C1，C2，C3，C4的a值依次为（ ）
图中曲线是对数函数y=logax的图象，已知a取$\sqrt{3}$，$\frac{4}{3}$，$\frac{3}{5}$，$\frac{1}{10}$四个值，则相应于C1，C2，C3，C4的a值依次为（ ）| A． | $\frac{4}{3}$，$\sqrt{3}$，$\frac{3}{5}$，$\frac{1}{10}$ | B． | $\sqrt{3}$，$\frac{4}{3}$，$\frac{1}{10}$，$\frac{3}{5}$ | C． | $\sqrt{3}$，$\frac{4}{3}$，$\frac{3}{5}$，$\frac{1}{10}$ | D． | $\frac{4}{3}$，$\sqrt{3}$，$\frac{1}{10}$，$\frac{3}{5}$ |
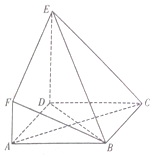如图，四边形ABCD是正方形，DE⊥平面ABCD，AF∥DE，AF=$\frac{1}{2}AD=\frac{1}{3}$ED=1．