题目内容
4.已知f(x)=2sin($\frac{x}{2}$+$\frac{π}{6}$)(1)若向量$\overrightarrow{m}$=($\sqrt{3}$cos$\frac{x}{4}$,cos$\frac{x}{4}$),$\overrightarrow{n}$=(-cos$\frac{x}{4}$,sin$\frac{x}{4}$),且$\overrightarrow{m}$∥$\overrightarrow{n}$,求f(x)的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足($\sqrt{2}$a-c)cosB=bcosC,求f(A)的取值范围.
分析 (1)利用数量积的坐标运算与辅助角公式得到:sin($\frac{x}{2}$+$\frac{π}{6}$)+$\frac{1}{2}$=0,从而可求f(x)的值;
(2)利用正弦定理求出A取值范围,然后求出函数f(A)的取值范围.
解答 解:(1)∵向量$\overrightarrow{m}$=($\sqrt{3}$cos$\frac{x}{4}$,cos$\frac{x}{4}$),$\overrightarrow{n}$=(-cos$\frac{x}{4}$,sin$\frac{x}{4}$),且$\overrightarrow{m}$∥$\overrightarrow{n}$,
∴$\sqrt{3}$cos$\frac{x}{4}$sin$\frac{x}{4}$+cos2$\frac{x}{4}$=$\frac{\sqrt{3}}{2}$sin$\frac{x}{2}$+$\frac{1}{2}$cos$\frac{x}{2}$+$\frac{1}{2}$=0,
∴sin($\frac{x}{2}$+$\frac{π}{6}$)+1=0,
∴sin($\frac{x}{2}$+$\frac{π}{6}$)=-1,
∴f(x)=-1;
(2)因为($\sqrt{2}$a-c)cosB=bcosC,
由正弦定理得:($\sqrt{2}$sinA-sinC)cosB=sinBcosC,
即$\sqrt{2}$sinAcosB=sinBcosC+sinBsinC=sin(B+C),
又△ABC中A+B+C=π,
∴$\sqrt{2}$sinAcosB=sinA,
∵A,B∈(0,π),
∴cosB=$\frac{\sqrt{2}}{2}$,则B=$\frac{π}{4}$,
因此A+C=$\frac{3π}{4}$,于是A∈(0,$\frac{3π}{4}$),
由f(x)=2sin($\frac{x}{2}$+$\frac{π}{6}$),得到:f(A)=2sin($\frac{A}{2}$+$\frac{π}{6}$),$\frac{π}{6}$<$\frac{A}{2}$+$\frac{π}{6}$<$\frac{13π}{24}$
故f(A)的取值范围为(1,2].
点评 本题考查数量积的坐标运算,考查三角函数中的恒等变换应用,突出考查辅助角公式与两角和的余弦,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
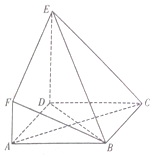 如图,四边形ABCD是正方形,DE⊥平面ABCD,AF∥DE,AF=$\frac{1}{2}AD=\frac{1}{3}$ED=1.
如图,四边形ABCD是正方形,DE⊥平面ABCD,AF∥DE,AF=$\frac{1}{2}AD=\frac{1}{3}$ED=1.