题目内容
已知tanα，tanβ分别是lg（6x2-5x+2）=0的两个实根，则tan（α+β）= ．
考点：两角和与差的正切函数
专题：三角函数的求值
分析：由条件利用一元二次方程根与系数的关系可得tanα+tanβ和tanα•tanβ的值，从而求得 tan（α+β）的值．
解答：
解：由题意lg（6x2-5x+2）=0，
可得6x2-5x+1=0，tanα，tanβ分别是lg（6x2-5x+2）=0的两个实根，
∴tanα+tanβ=
，tanα•tanβ=
，
∴tan（α+β）=
=
=1．
故答案为：1．
可得6x2-5x+1=0，tanα，tanβ分别是lg（6x2-5x+2）=0的两个实根，
∴tanα+tanβ=
| 5 |
| 6 |
| 1 |
| 6 |
∴tan（α+β）=
| tanα+tanβ |
| 1-tanα•tanβ |
| ||
1-
|
故答案为：1．
点评：本题主要考查一元二次方程根与系数的关系，两角和的正切公式的应用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
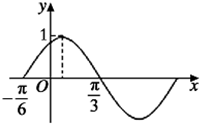如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜
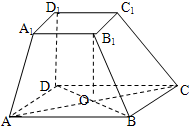如图，在四棱台ABCD-A1B1C1D1中，DD1⊥平面ABCD，底面ABCD是平行四边形，AB=AD=2A1B1，∠BAD=60°