题目内容
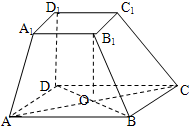 如图,在四棱台ABCD-A1B1C1D1中,DD1⊥平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°
如图,在四棱台ABCD-A1B1C1D1中,DD1⊥平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°(1)证明:BB1⊥AC;
(2)若AB=2,且二面角A1-AB-C大小为60°,连接AC,BD,设交点为O,连接B1O.求三棱锥B1-ABO外接球的体积.
(球体体积公式:V=
| 4 |
| 3 |
考点:与二面角有关的立体几何综合题,球的体积和表面积
专题:空间位置关系与距离
分析:(1)底面平行四边形ABCD中,AB=AD,可得四边形ABCD是菱形,可得AC⊥BD,又DD1⊥平面ABCD,可得DD1⊥AC,因此AC⊥平面BDD1,即可证明.
(2)四边形ABCD为平行四边形,可得OD=
BD.由棱台定义及AB=AD=2A1B1知D1B1∥DO,且D1B1=DO,可证:边四形D1B1OD为平行四边形,得到DD1∥B1O.
可得B1O⊥平面ABCD,即B1O⊥AO,B1O⊥BO.由(1)知AC⊥BD于点O,即AO⊥BO,以DB,AC,OB1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系如图,
设B1(0,0,h),则D1(-1,0,h);设A1(a,b,h) (h>0).则
=(1,-
,0),
=(a+1,b,0),设平面A1AB的一个法向量为
=(x,y,z),则
,可得
,又已知平面ABC的一个法向量
=(0,0,1)由二面角A1-AB-C大小为60°,可得|cos<
,
>|=
=
,解得h.利用三棱锥B1-ABO外接球的直径就是以OA,OB,OB1为三条棱的长方体的体对角线,求出即可得出.
(2)四边形ABCD为平行四边形,可得OD=
| 1 |
| 2 |
可得B1O⊥平面ABCD,即B1O⊥AO,B1O⊥BO.由(1)知AC⊥BD于点O,即AO⊥BO,以DB,AC,OB1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系如图,
设B1(0,0,h),则D1(-1,0,h);设A1(a,b,h) (h>0).则
| DA |
| 3 |
| D1A1 |
| n |
|
| n |
| m |
| n |
| m |
| ||||
|
| 1 |
| 2 |
解答:
(1)证明:底面平行四边形ABCD中,连接AC,BD,设AC∩BD=O,
∵AB=AD,∴四边形ABCD是菱形,
∴AC⊥BD,
又DD1⊥平面ABCD,
∴DD1⊥AC,又BD∩DD1=D,
∴AC⊥平面BDD1,
又∵四棱台ABCD-A1B1C1D1中,侧棱DD1与BB1延长后交于一点,
∴BB1?平面BDD1,∴AC⊥BB1.即BB1⊥AC.
(2)解:∵四边形ABCD为平行四边形,∴OD=
BD.
由棱台定义及AB=AD=2A1B1知D1B1∥DO,且D1B1=DO,
∴边四形D1B1OD为平行四边形,∴DD1∥B1O.
∵DD1⊥平面ABCD,
∴B1O⊥平面ABCD,即B1O⊥AO,B1O⊥BO.
由(1)知AC⊥BD于点O,即AO⊥BO
以DB,AC,OB1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系如图:则
A(0,-
,0),B(1,0,0),D(-1,0,0),设B1(0,0,h),则D1(-1,0,h);设A1(a,b,h) (h>0)
则
=(1,-
,0),
=(a+1,b,0),
∵
=
,
∴a=-
,b=-
.即A1(-
,-
,h).
∴
=(-
,
,h),
=(1,
,0)
设平面A1AB的一个法向量为
=(x,y,z),
则
,即
取y=
,则x=-3,z=-
即
=(-3,
,-
),
又已知平面ABC的一个法向量
=(0,0,1),
由二面角A1-AB-C大小为60°,可得|cos<
,
>|=
=
,
解得:h=
即棱台的高为
∵B1O⊥AO,B1O⊥BO,AO⊥BO,
∴三棱锥B1-ABO外接球的直径就是以OA,OB,OB1为三条棱的长方体的体对角线,长为
=
,
∴外接球半径R=
,
∴外接球体积为V=
πR3=
π×(
)3=
.

∵AB=AD,∴四边形ABCD是菱形,
∴AC⊥BD,
又DD1⊥平面ABCD,
∴DD1⊥AC,又BD∩DD1=D,
∴AC⊥平面BDD1,
又∵四棱台ABCD-A1B1C1D1中,侧棱DD1与BB1延长后交于一点,
∴BB1?平面BDD1,∴AC⊥BB1.即BB1⊥AC.
(2)解:∵四边形ABCD为平行四边形,∴OD=
| 1 |
| 2 |
由棱台定义及AB=AD=2A1B1知D1B1∥DO,且D1B1=DO,
∴边四形D1B1OD为平行四边形,∴DD1∥B1O.
∵DD1⊥平面ABCD,
∴B1O⊥平面ABCD,即B1O⊥AO,B1O⊥BO.
由(1)知AC⊥BD于点O,即AO⊥BO
以DB,AC,OB1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系如图:则
A(0,-
| 3 |
则
| DA |
| 3 |
| D1A1 |
∵
| D1A1 |
| 1 |
| 2 |
| DA |
∴a=-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴
| AA1 |
| 1 |
| 2 |
| ||
| 2 |
| AB |
| 3 |
设平面A1AB的一个法向量为
| n |
则
|
|
取y=
| 3 |
| 3 |
| h |
即
| n |
| 3 |
| 3 |
| h |
又已知平面ABC的一个法向量
| m |
由二面角A1-AB-C大小为60°,可得|cos<
| n |
| m |
| ||||
|
| 1 |
| 2 |
解得:h=
| 3 |
| 2 |
| 3 |
| 2 |
∵B1O⊥AO,B1O⊥BO,AO⊥BO,
∴三棱锥B1-ABO外接球的直径就是以OA,OB,OB1为三条棱的长方体的体对角线,长为
(
|
| 5 |
| 2 |
∴外接球半径R=
| 5 |
| 4 |
∴外接球体积为V=
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 4 |
| 125π |
| 48 |
点评:本题考查了向量相互垂直与数量积的关系证明线面垂直、利用法向量的夹角求出二面角的方法、长方体外接球的体积计算公式、平行四边形与菱形的性质,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
设a,b,c,A,B,C为非零常数,则“ax2+bx+c>0与Ax2+Bx+C>0解集相同”是“
=
=
”的( )
| a |
| A |
| b |
| B |
| c |
| C |
| A、既不充分也不必要条件 |
| B、充分必要条件 |
| C、必要而不充分条件 |
| D、充分而不必要条件 |
若a=20.5,b=ln2,c=0.5e(e是自然对数的底),则( )
| A、a<b<c |
| B、b>a>c |
| C、a>c>b |
| D、a>b>c |
已知i是虚数单位,m和n都是实数,且m(1+i)=
+ni,则(
)2015=( )
| 3 |
| m+ni |
| m-ni |
| A、-1 | B、1 | C、-i | D、i |
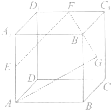 如图,正方体ABCD-A1B1C1D1中,E、F分别是A1A,C1D1的中点,G为正方形BCC1B1的中心,则四边形AEFG在该正方体的各个面的投影不可能是( )
如图,正方体ABCD-A1B1C1D1中,E、F分别是A1A,C1D1的中点,G为正方形BCC1B1的中心,则四边形AEFG在该正方体的各个面的投影不可能是( )