题目内容
求函数y=2cos2x+5sinx-4的值域.
考点:三角函数的最值
专题:三角函数的求值
分析:令t=sinx(-1≤t≤1)换元,然后利用二次函数的单调性求得函数的值域.
解答:
解:y=2cos2x+5sinx-4
=2(1-sin2x)+5sinx-4
=-2sin2x+5sinx-2.
令t=sinx(-1≤t≤1).
则y=-t2+5t-2(-1≤t≤1),
函数y=-t2+5t-2在[-1,1]上为增函数,
∴当t=-1时,ymin=-(-1)2+5×(-1)-2=-8;
当t=1时,ymax=-12+5×1-2=2.
∴函数y=2cos2x+5sinx-4的值域为[-8,2].
=2(1-sin2x)+5sinx-4
=-2sin2x+5sinx-2.
令t=sinx(-1≤t≤1).
则y=-t2+5t-2(-1≤t≤1),
函数y=-t2+5t-2在[-1,1]上为增函数,
∴当t=-1时,ymin=-(-1)2+5×(-1)-2=-8;
当t=1时,ymax=-12+5×1-2=2.
∴函数y=2cos2x+5sinx-4的值域为[-8,2].
点评:本题考查了换元法求函数的值域,是基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
函数y=sin(x+φ)的图象关于y轴对称的充分必要条件是( )
A、φ=
| ||
| B、φ=π | ||
C、φ=kπ+
| ||
D、φ=2kπ+
|
已知a>b>0,二次函数f(x)=ax2+2x+b有且仅有一个零点,则
的最小值为( )
| a2+b2 |
| a-b |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
设a,b,c,A,B,C为非零常数,则“ax2+bx+c>0与Ax2+Bx+C>0解集相同”是“
=
=
”的( )
| a |
| A |
| b |
| B |
| c |
| C |
| A、既不充分也不必要条件 |
| B、充分必要条件 |
| C、必要而不充分条件 |
| D、充分而不必要条件 |
设条件p:a≥0;条件q:a2+a≥0,那么p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
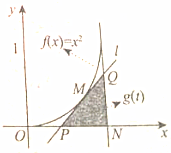 如图,抛物线f(x)=x2(0<x<1)在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交于点P,Q,直线x=1与x轴的交点为N,设△PQN的面积为g(t)
如图,抛物线f(x)=x2(0<x<1)在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交于点P,Q,直线x=1与x轴的交点为N,设△PQN的面积为g(t)