题目内容
已知集合A={x|y=lg（x+1）}，B={y=|y=1-ex，x∈R}，则A∩B= ．
考点：交集及其运算
专题：集合
分析：求出集合A，B的等价条件，利用集合的基本运算进行求解．
解答：
解：A={x|y=lg（x+1）}={x|x+1＞0}={x|x＞-1}，
B={y|y=1-ex，x∈R}={y|y＜1}，
则A∩B={x|-1＜x＜1}，
故答案为：（-1，1）
B={y|y=1-ex，x∈R}={y|y＜1}，
则A∩B={x|-1＜x＜1}，
故答案为：（-1，1）
点评：本题主要考查集合的基本运算，根据条件求出集合A，B是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知i是虚数单位，m和n都是实数，且m（1+i）=
+ni，则（
）2015=（ ）
| 3 |
| m+ni |
| m-ni |
| A、-1 | B、1 | C、-i | D、i |
设条件p：a≥0；条件q：a2+a≥0，那么p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若P={y|y≥0}，Q={x|-
≤x≤
}，则P∩Q=（ ）
| 2 |
| 2 |
A、{0，
| ||||
| B、{（1，1），（-1，-1）} | ||||
C、[0，
| ||||
D、[-
|
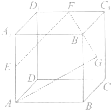如图，正方体ABCD-A1B1C1D1中，E、F分别是A1A，C1D1的中点，G为正方形BCC1B1的中心，则四边形AEFG在该正方体的各个面的投影不可能是（ ）
