题目内容
某工厂要建造一个长方体形有盖贮水池，其容积为48m3，深为3m．如果池壁每平方米的造价为100元，上盖与下底每平方米的造价为120元，怎样设计水池的长和宽能使总造价最低？最低总造价是多少？
考点：函数模型的选择与应用
专题：应用题,函数的性质及应用
分析：设底面的长与宽分别为xm，ym，水池总造价为z元，建立函数关系式，求出z的最小值．
解答：
解：设底面的长为xm，宽为ym，水池总造价为z元，-------（1分）
则由容积为48m3，可得：3xy=48，因此xy=16-------（3分）
z=120×16×2+100（2×3x+2×3y）=3840+600（x+y）≥3840+600•2
=8640
当且仅当x=y=4时，取等号---------（11分）
所以，将水池的地面设计成边长为40m的正方形时总造价最低，最低总造价为8640元．-------（12分）
则由容积为48m3，可得：3xy=48，因此xy=16-------（3分）
z=120×16×2+100（2×3x+2×3y）=3840+600（x+y）≥3840+600•2
| xy |
当且仅当x=y=4时，取等号---------（11分）
所以，将水池的地面设计成边长为40m的正方形时总造价最低，最低总造价为8640元．-------（12分）
点评：此题首先需要由实际问题向数学问题转化，即建立函数关系式，然后求函数的最值，其中用到了均值不等式定理．
练习册系列答案
名校课堂系列答案
相关题目
六个棱长为1的正方体在桌面上堆叠成一个几何体，该几何体的正视图与俯视图如图所示，则其左视图不可能为（ ）
关于函数y=sin（2x+
）的图象，有以下四个说法：
①关于点（
，0）对称；
②关于点（
，0）对称；
③关于直线x=
对称；
④关于直线x=
对称
则正确的是（ ）
| π |
| 6 |
①关于点（
| π |
| 6 |
②关于点（
| 5π |
| 12 |
③关于直线x=
| π |
| 6 |
④关于直线x=
| 5π |
| 12 |
则正确的是（ ）
| A、①③ | B、②③ | C、①④ | D、②④ |
如图所示的程序框图，其输出的结果是（ ）
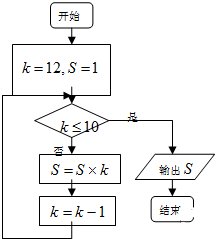
| A、11 | B、12 |
| C、131 | D、132 |
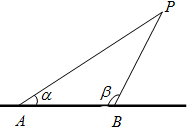根据国际公法，外国船只不得进入离我国海岸线12海里以内的区域（此为我国领海，含分界线）．若外国船只进入我国领海，我方将向其发出警告令其退出．如图，已知直线AB为海岸线，A，B是相距12海里的两个观测站，现发现一外国船只航行于点P处，此时我方测得∠BAP=α，∠ABP=β（0＜α＜π，0＜β＜π）．