题目内容
求经过原点且与直线x=1及圆:(x-1)2+(y-2)2=1都相切的圆的标准方程.
考点:椭圆的简单性质
专题:计算题,直线与圆
分析:设圆的方程为(x-a)2+(y-b)2=r2(r>0),利用圆过原点,可得a2+b2=r2,圆与直线x=1相切,可得(a-1)2=r2,两圆外切,可得(a-1)2+(b-2)2=(r+1)2,即可求出圆的标准方程.
解答:
解:设圆的方程为(x-a)2+(y-b)2=r2(r>0)
∵圆过原点,∴a2+b2=r2,
∵圆与直线x=1相切,∴(a-1)2=r2,
又∵原点在已知圆的外部,而欲求之圆要过原点,故两圆只能外切,
∴(a-1)2+(b-2)2=(r+1)2,
从而a=
,b=
,r2=
,
∴圆的方程是(x-
)2+(y-
)2=
.
∵圆过原点,∴a2+b2=r2,
∵圆与直线x=1相切,∴(a-1)2=r2,
又∵原点在已知圆的外部,而欲求之圆要过原点,故两圆只能外切,
∴(a-1)2+(b-2)2=(r+1)2,
从而a=
| 3 |
| 8 |
| 1 |
| 2 |
| 25 |
| 64 |
∴圆的方程是(x-
| 3 |
| 8 |
| 1 |
| 2 |
| 25 |
| 64 |
点评:本题考查圆的标准方程,考查学生的计算能力,考查待定系数法的运用,比较基础.

练习册系列答案
相关题目
已知cosα=
,且0<α<π,则tan(α+
)=( )
| 4 |
| 5 |
| π |
| 4 |
A、
| ||
| B、7 | ||
C、-
| ||
| D、-7 |
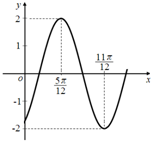 已知函数f(x)=Asin(ωx-
已知函数f(x)=Asin(ωx- 如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,PA=3,AD=2,AB=4,∠ABC=60°.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,PA=3,AD=2,AB=4,∠ABC=60°.