题目内容
关于函数y=sin（2x+
）的图象，有以下四个说法：
①关于点（
，0）对称；
②关于点（
，0）对称；
③关于直线x=
对称；
④关于直线x=
对称
则正确的是（ ）
| π |
| 6 |
①关于点（
| π |
| 6 |
②关于点（
| 5π |
| 12 |
③关于直线x=
| π |
| 6 |
④关于直线x=
| 5π |
| 12 |
则正确的是（ ）
| A、①③ | B、②③ | C、①④ | D、②④ |
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：利用正弦函数的图象的对称性考查各个选项是否正确，从个人得出结论．
解答：
解：关于函数y=sin（2x+
），当x=
时，求得y=1，为函数的最大值，
故函数的图象关于直线x=
对称，故③正确且①不正确．
令x=
，求得y=0，故函数的图象关于点（
，0）对称，故②正确且④不正确，
故选：B．
| π |
| 6 |
| π |
| 6 |
故函数的图象关于直线x=
| π |
| 6 |
令x=
| 5π |
| 12 |
| 5π |
| 12 |
故选：B．
点评：本题主要考查正弦函数的图象的对称性，属于基础题．
练习册系列答案
相关题目
若0＜a＜
，则下列不等式中正确的是（ ）
| 1 |
| 2 |
A、loga（1-
| ||
B、ax≤（
| ||
| C、cos（1+α）＜cos（1-α） | ||
| D、（1-a）n＜an（n∈N*） |
函数f（x）=
+lg（3x-1）的定义域是（ ）
| x2-1 | ||
|
| A、（-∞，-1） | ||
B、（-1，
| ||
C、（-
| ||
D、（
|
已知cosα=
，且0＜α＜π，则tan（α+
）=（ ）
| 4 |
| 5 |
| π |
| 4 |
A、
| ||
| B、7 | ||
C、-
| ||
| D、-7 |
已知
=（cosα，sinα），
=（1，-1），α∈[-
，0]，则
与
夹角的取值范围为（ ）
| OA |
| OB |
| π |
| 2 |
| OA |
| OB |
A、（0，
| ||||
B、（
| ||||
C、[0，
| ||||
D、[
|
一批产品中，有10件正品和5件次品，对产品逐个进行检测，如果已检测到前3次均为正品，则第4次检测的产品仍为正品的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知全集U=R，集合A={0，1，2，3，4，5}，B=[2，+∞），则图中阴影部分所表示的集合（ ）
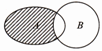
| A、{1} |
| B、{0，1} |
| C、{1，2} |
| D、{0，1，2} |
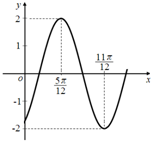已知函数f（x）=Asin（ωx-