题目内容
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参见而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为
,且各局胜负相互独立.求:
(Ⅰ)恰好打满2局比赛就停止的概率;
(Ⅱ)比赛停止时已打局数ξ的分布列与期望Eξ.
| 1 |
| 2 |
(Ⅰ)恰好打满2局比赛就停止的概率;
(Ⅱ)比赛停止时已打局数ξ的分布列与期望Eξ.
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)令Ak,Bk,Ck分别表示甲、乙、丙在第k局中获胜,且它们都是相互独立的,由此能求出恰好打满2局比赛就停止的概率.
(Ⅱ)ξ的所有可能值为2,3,4,5,6,分别求出相应的概率,由此能求出比赛停止时已打局数ξ的分布列与期望Eξ.
(Ⅱ)ξ的所有可能值为2,3,4,5,6,分别求出相应的概率,由此能求出比赛停止时已打局数ξ的分布列与期望Eξ.
解答:
解:(Ⅰ)令Ak,Bk,Ck分别表示甲、乙、丙在第k局中获胜,
且它们都是相互独立的,
恰好打满2局比赛就停止的概率为:
P(A1A2)+P(B1B2)=
+
=
.(5分)
(Ⅱ)ξ的所有可能值为2,3,4,5,6,
由(Ⅰ)有P(ξ=2)=
,
P(ξ=3)=P(A1C2C3)+P(B1C2C3)=
+
=
,
P(ξ=4)=P(A1C2B3B4)+P(B1C2A3A4)=
+
=
,
P(ξ=5)=P(A1C2B3A4A5)+P(B1C2A3B4B5)=
+
=
,
P(ξ=6)=P(A1C2B3A4C5)+P(B1C2A3B4C5)=
+
=
.
故有分布列为
∴Eξ=2×
+3×
+4×
+5×
+6×
=
(局).(13分)
且它们都是相互独立的,
恰好打满2局比赛就停止的概率为:
P(A1A2)+P(B1B2)=
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 2 |
(Ⅱ)ξ的所有可能值为2,3,4,5,6,
由(Ⅰ)有P(ξ=2)=
| 1 |
| 2 |
P(ξ=3)=P(A1C2C3)+P(B1C2C3)=
| 1 |
| 23 |
| 1 |
| 23 |
| 1 |
| 4 |
P(ξ=4)=P(A1C2B3B4)+P(B1C2A3A4)=
| 1 |
| 24 |
| 1 |
| 24 |
| 1 |
| 8 |
P(ξ=5)=P(A1C2B3A4A5)+P(B1C2A3B4B5)=
| 1 |
| 25 |
| 1 |
| 25 |
| 1 |
| 16 |
P(ξ=6)=P(A1C2B3A4C5)+P(B1C2A3B4C5)=
| 1 |
| 25 |
| 1 |
| 25 |
| 1 |
| 16 |
故有分布列为
| ξ | 2 | 3 | 4 | 5 | 6 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 16 |
| 47 |
| 16 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法.

练习册系列答案
相关题目
当你到一个红绿灯路口时,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为45秒,那么你看到黄灯的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一批产品中,有10件正品和5件次品,对产品逐个进行检测,如果已检测到前3次均为正品,则第4次检测的产品仍为正品的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
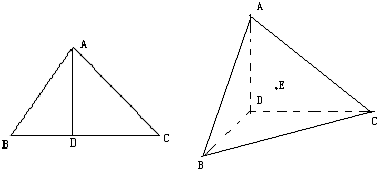 如图,∠ACB=45°,BC=6过A作AD⊥BC,垂足D在线段BC上且异于点B,沿AD将△ABD折起,组成三棱锥A-BCD,过点D作DE⊥平面ABC,且点E为三角形ABC的垂心.
如图,∠ACB=45°,BC=6过A作AD⊥BC,垂足D在线段BC上且异于点B,沿AD将△ABD折起,组成三棱锥A-BCD,过点D作DE⊥平面ABC,且点E为三角形ABC的垂心.