题目内容
等差数列{an}的前n项的和为Sn,且S7-S4=4π,则tana6=( )
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知条件利用等差数列的前n项和公式求出3a1+15d=4π,从而得到a6=a1+5d=
π,由此能求出tana6.
| 4 |
| 3 |
解答:
解:∵等差数列{an}的前n项的和为Sn,且S7-S4=4π,
∴(7a1+
d)-(4a1 +
d)
=3a1+15d=4π,
∴a6=a1+5d=
π,
∴tana6=tan
π=tan
=
.
故选:C.
∴(7a1+
| 7×6 |
| 2 |
| 4×3 |
| 2 |
=3a1+15d=4π,
∴a6=a1+5d=
| 4 |
| 3 |
∴tana6=tan
| 4 |
| 3 |
| π |
| 3 |
| 3 |
故选:C.
点评:本题考查数列的第六项的正切值的求法,是基础题,解题时要注意等差数列的性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
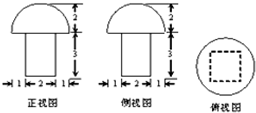
一个几何体的三视图如图所示,这个几何体的体积是( )

A、
| ||
B、
| ||
C、12+
| ||
D、3+
|
数列{an}共有11项,a1=0,a11=4,且|ak+1-ak|=1(k=1,2,…,10),则满足该条件的不同数列的个数为( )
| A、100 | B、120 |
| C、140 | D、160 |
已知复数ω=-
+
i(i为虚数单位),则ω4等于( )
| 1 |
| 2 |
| ||
| 2 |
| A、1 | ||||||
B、-
| ||||||
C、
| ||||||
D、
|
设实数x,y满足不等式组
,则z=x-2y的最小值是( )
|
| A、-8 | ||
| B、-6 | ||
| C、-3 | ||
D、-
|
设等差数列{an}的前n项和为Sn,若a1=1,a2+a3=11,则S6-S3=( )
| A、27 | B、39 | C、45 | D、63 |