题目内容
已知全集U=R,则正确表示集合M={x|x2+2x>0}和 N={-2,-1,0}关系的韦恩(Venn)图是( )
A、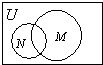 |
B、 |
C、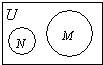 |
D、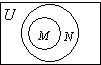 |
考点:Venn图表达集合的关系及运算
专题:集合
分析:解不等式求出M={x|x>0或x<-2},进而可得M∩N=∅,比照四个答案中的图形,可得答案.
解答:
解:∵集合M={x|x2+2x>0}={x|x>0或x<-2},
集合N={-2,-1,0},
∴M∩N=∅,
故选:C
集合N={-2,-1,0},
∴M∩N=∅,
故选:C
点评:本题考查的知识点是Venn图表达集合的关系及运算,其中根据已知分析出M∩N=∅,是解答的关键.

练习册系列答案
相关题目
若集合A={x|2x<1},B={x|x2-x≤0},则(∁RA)∩B=( )
| A、{x|0<x<1} |
| B、{x|0≤x<1} |
| C、{x|0<x≤1} |
| D、{x|0≤x≤1} |
设O为△ABC内部的一点,且
+
+2
=0,则△AOC的面积与△BOC的面积之比为( )
| OA |
| OB |
| OC |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
复数z=
(i为虚数单位),则z的共轭复数
为( )
| 2 |
| 1-i |
. |
| z |
| A、1-i | B、1+i |
| C、3-i | D、3+i |
等差数列{an}的前n项的和为Sn,且S7-S4=4π,则tana6=( )
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
若0<
<
的解集记为p,关于x的不等式x2+(a-1)x-a>0的解集记为q,且p是q的充分不必要条件,则实数a的取值范围是( )
| 1 |
| x |
| 1 |
| 2 |
| A、(-2,-1] |
| B、[-2,-1] |
| C、[-1,+∞) |
| D、[-2,+∞) |
设曲线C的参数方程为
(t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为( )
|
| A、sinθ=ρcos2θ |
| B、sinθ=ρcosθ |
| C、2sinθ=ρcos2θ |
| D、sinθ=2ρcos2θ |