题目内容
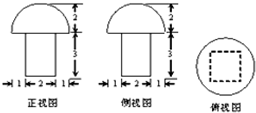
一个几何体的三视图如图所示，这个几何体的体积是（ ）
A、
| ||
B、
| ||
C、12+
| ||
D、3+
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可知，该几何体是一个半球和四棱柱结合而成的组合体，分别求出半球和四棱柱的体积，相加可得答案．
解答：
解：由已知中的三视图可知，该几何体是一个半球和四棱柱结合而成的组合体，
其中半球的半径为2，故半径的体积为
×π×23=
π，
四棱柱的底面是一个边长为2的正方形，高为3，
故四棱柱的体积为2×2×3=12，
故组合体的体积为：12+
π，
故选：C
其中半球的半径为2，故半径的体积为
| 2 |
| 3 |
| 16 |
| 3 |
四棱柱的底面是一个边长为2的正方形，高为3，
故四棱柱的体积为2×2×3=12，
故组合体的体积为：12+
| 16 |
| 3 |
故选：C
点评：本题考查的知识点是由三视图求体积，其中根据已知中的三视图分析出几何体的形状是解答的关键．
练习册系列答案
相关题目
函数y=sin（ωx+φ）（ω＞0，|φ|＜集合A={x|2x-x2＞0}，B={x|1≤x＜2}，则∁AB=（ ）
| A、（0，1） |
| B、（0，1] |
| C、[0，1] |
| D、（1，2） |
若集合A={x|2x＜1}，B={x|x2-x≤0}，则（∁RA）∩B=（ ）
| A、{x|0＜x＜1} |
| B、{x|0≤x＜1} |
| C、{x|0＜x≤1} |
| D、{x|0≤x≤1} |
设O为△ABC内部的一点，且
+
+2
=0，则△AOC的面积与△BOC的面积之比为（ ）
| OA |
| OB |
| OC |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
等差数列{an}的前n项的和为Sn，且S7-S4=4π，则tana6=（ ）
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
已知向量
=（1，2），
=（2，-1），下列结论中不正确的是（ ）
| a |
| b |
A、|
| ||||||||
B、
| ||||||||
C、|
| ||||||||
D、
|