题目内容
已知复数ω=-
+
i(i为虚数单位),则ω4等于( )
| 1 |
| 2 |
| ||
| 2 |
| A、1 | ||||||
B、-
| ||||||
C、
| ||||||
D、
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:直接利用“1”的立方虚根的性质 求解即可.
解答:
解:∵复数ω=-
+
i是“1”的立方虚根,
∴ω3=1,
∴ω4=ω3•ω=ω=-
+
i.
故选:B.
| 1 |
| 2 |
| ||
| 2 |
∴ω3=1,
∴ω4=ω3•ω=ω=-
| 1 |
| 2 |
| ||
| 2 |
故选:B.
点评:本题考查复数的代数形式的混合运算,复数的立方虚根的性质,基本知识的考查.

练习册系列答案
相关题目
若集合A={x|2x<1},B={x|x2-x≤0},则(∁RA)∩B=( )
| A、{x|0<x<1} |
| B、{x|0≤x<1} |
| C、{x|0<x≤1} |
| D、{x|0≤x≤1} |
复数z=
(i为虚数单位),则z的共轭复数
为( )
| 2 |
| 1-i |
. |
| z |
| A、1-i | B、1+i |
| C、3-i | D、3+i |
等差数列{an}的前n项的和为Sn,且S7-S4=4π,则tana6=( )
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
 某校为了解网瘾学生上网情况,抽查了100名同学,统计他们暑假期间每天平均上网时间,绘成频率分布直方图(如图).则这100名同学中每天平均上网时间在6~8小时内的同学人数为( )
某校为了解网瘾学生上网情况,抽查了100名同学,统计他们暑假期间每天平均上网时间,绘成频率分布直方图(如图).则这100名同学中每天平均上网时间在6~8小时内的同学人数为( )| A、30 | B、40 | C、50 | D、60 |
若0<
<
的解集记为p,关于x的不等式x2+(a-1)x-a>0的解集记为q,且p是q的充分不必要条件,则实数a的取值范围是( )
| 1 |
| x |
| 1 |
| 2 |
| A、(-2,-1] |
| B、[-2,-1] |
| C、[-1,+∞) |
| D、[-2,+∞) |
已知三棱锥的三视图如图所示,则它的体积为( )
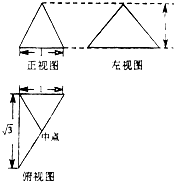

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=sinx(x∈[0,π]),在区间[0,π]上任取一点x0,则f(x0)≥
的概率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|