题目内容
设函数f(x)=
-ax,e为自然对数的底数
(Ⅰ)若函数f(x)的图象在点 (e2,f(e2))处的切线方程为 3x+4y-e2=0,求实数a,b的值;
(Ⅱ)当b=1时,若存在 x1,x2∈[e,e2],使 f(x1)≤f′(x2)+a成立,求实数a的最小值.
| bx |
| lnx |
(Ⅰ)若函数f(x)的图象在点 (e2,f(e2))处的切线方程为 3x+4y-e2=0,求实数a,b的值;
(Ⅱ)当b=1时,若存在 x1,x2∈[e,e2],使 f(x1)≤f′(x2)+a成立,求实数a的最小值.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(I)f′(x)=
-a(x>0,且x≠1),由题意可得f′(e2)=
-a=-
,f(e2)=
-ae2=-
e2,联立解得即可.
(II)当b=1时,f(x)=
-ax,f′(x)=
-a,由x∈[e,e2],可得
∈[
,1].由f′(x)+a=
=-(
-
)2+
≤
,可得[f′(x)+a]max=
,x∈[e,e2].存在 x1,x2∈[e,e2],使 f(x1)≤f′(x2)+a成立?x∈[e,e2],f(x)min≤f(x)max+a=
,对a分类讨论解出即可.
| b(lnx-1) |
| (lnx)2 |
| b |
| 4 |
| 3 |
| 4 |
| be2 |
| 2 |
| 1 |
| 2 |
(II)当b=1时,f(x)=
| x |
| lnx |
| lnx-1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| 2 |
| lnx-1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:(I)f′(x)=
-a(x>0,且x≠1),
∵函数f(x)的图象在点 (e2,f(e2))处的切线方程为 3x+4y-e2=0,
∴f′(e2)=
-a=-
,f(e2)=
-ae2=-
e2,
联立解得a=b=1.
(II)当b=1时,f(x)=
-ax,f′(x)=
-a,
∵x∈[e,e2],∴lnx∈[1,2],
∈[
,1].
∴f′(x)+a=
=-(
-
)2+
≤
,
∴[f′(x)+a]max=
,x∈[e,e2].
存在 x1,x2∈[e,e2],使 f(x1)≤f′(x2)+a成立?x∈[e,e2],f(x)min≤f(x)max+a=
,
①当a≥
时,f′(x)≤0,f(x)在x∈[e,e2]上为减函数,则f(x)min=f(e2)=
-ae2≤
,解得a≥
-
.
②当a<
时,由f′(x)=-(
-
)2+
-a在[e,e2]上的值域为[-a,
-a].
(i)当-a≥0即a≤0时,f′(x)≥0在x∈[e,e2]上恒成立,因此f(x)在x∈[e,e2]上为增函数,
∴f(x)min=f(e)=e-ae≥e>
,不合题意,舍去.
(ii)当-a<0时,即0<a<
时,由f′(x)的单调性和值域可知:存在唯一x0∈(e,e2),使得f′(x0)=0,
且满足当x∈[e,x0),f′(x)<0,f(x)为减函数;当x∈(x0,e2)时,f′(x)>0,f(x)为增函数.
∴f(x)min=f(x0)=
-ax0≤
,x0∈(e,e2).
∴a≥
-
>
-
>
,与0<a<
矛盾.
综上可得:a的最小值为
-
.
| b(lnx-1) |
| (lnx)2 |
∵函数f(x)的图象在点 (e2,f(e2))处的切线方程为 3x+4y-e2=0,
∴f′(e2)=
| b |
| 4 |
| 3 |
| 4 |
| be2 |
| 2 |
| 1 |
| 2 |
联立解得a=b=1.
(II)当b=1时,f(x)=
| x |
| lnx |
| lnx-1 |
| (lnx)2 |
∵x∈[e,e2],∴lnx∈[1,2],
| 1 |
| lnx |
| 1 |
| 2 |
∴f′(x)+a=
| lnx-1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴[f′(x)+a]max=
| 1 |
| 4 |
存在 x1,x2∈[e,e2],使 f(x1)≤f′(x2)+a成立?x∈[e,e2],f(x)min≤f(x)max+a=
| 1 |
| 4 |
①当a≥
| 1 |
| 4 |
| e2 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4e2 |
②当a<
| 1 |
| 4 |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
(i)当-a≥0即a≤0时,f′(x)≥0在x∈[e,e2]上恒成立,因此f(x)在x∈[e,e2]上为增函数,
∴f(x)min=f(e)=e-ae≥e>
| 1 |
| e |
(ii)当-a<0时,即0<a<
| 1 |
| 4 |
且满足当x∈[e,x0),f′(x)<0,f(x)为减函数;当x∈(x0,e2)时,f′(x)>0,f(x)为增函数.
∴f(x)min=f(x0)=
| x0 |
| lnx0 |
| 1 |
| 4 |
∴a≥
| 1 |
| lnx0 |
| 1 |
| 4x0 |
| 1 |
| lne2 |
| 1 |
| 4e2 |
| 1 |
| 4 |
| 1 |
| 4 |
综上可得:a的最小值为
| 1 |
| 2 |
| 1 |
| 4e2 |
点评:本题考查了利用导数研究函数的单调性极值与最值、切线,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
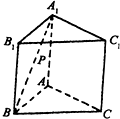 如图,已知正三棱柱ABC-A1B1C1的各棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各棱长都为a,P为A1B上的点.