题目内容
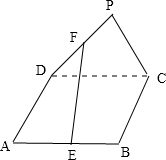如图，点P为正方形ABCD所在平面外的一点，E、F分别是AB、PD的中点．求证：EF∥平面PBC．考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：做DA的中点M，连接MF，ME，通过中位线的性质证明出EM∥BC，MF∥PC，进而根据线面平行的判定定理、面面平行的判定定理证明出面MEF∥面ABP，继而根据面面平行的性质证明出EF∥平面PBC．
解答：
证明：做DA的中点M，连接MF，ME，如图
∵E、F、M均为中点，
∴EM∥BC，MF∥PC，
∵BC?平面PBC，PC?平面PBC，BC∩PC=C，
∴面MEF∥面PBC，
∵EF?面MEF，
∴EF∥平面PBC．
∵E、F、M均为中点，
∴EM∥BC，MF∥PC，
∵BC?平面PBC，PC?平面PBC，BC∩PC=C，
∴面MEF∥面PBC，
∵EF?面MEF，
∴EF∥平面PBC．
点评：本题主要考查了线面平行判定定理的应用．考查了学生的空间想象能力．
练习册系列答案
教材全解字词句篇系列答案
相关题目
如图所示，四棱锥P-ABCD，底面四边形ABCD是正方形，侧面PCD是边长为a的正三角形，且平面PCD⊥底面ABCD，E为PC的中点．
如图，已知正三棱柱ABC-A1B1C1的各棱长都为a，P为A1B上的点．