题目内容
设a>2,A=
+
,B=
+
,则A、B的大小关系是( )
| a+1 |
| a |
| a+2 |
| a-2 |
| A、A>B | B、A<B |
| C、A≥B | D、A≤B |
考点:不等式比较大小
专题:不等式的解法及应用
分析:利用“平方作差法”即可得出.
解答:
解:∵a>2,A=
+
,B=
+
,
∴A2-B2=2a+1+2
-[2a+2
]
=1+2
-2
,
∵(1+2
)2-(2
)2
=4a+13+4
>0,
∴1+2
-2
>0,
∴A>B.
故选:A.
| a+1 |
| a |
| a+2 |
| a-2 |
∴A2-B2=2a+1+2
| a(a+1) |
| a2-4 |
=1+2
| a2+a |
| a2-4 |
∵(1+2
| a(a+1) |
| a2-4 |
=4a+13+4
| a2+a |
∴1+2
| a2+a |
| a2-4 |
∴A>B.
故选:A.
点评:本题考查了“平方作差法”比较两个数的大小,属于基础题.

练习册系列答案
相关题目
下列函数中值域为R的函数有( )
①y=(
)x ②y=x2 ③y=
④y=log2x.
①y=(
| 1 |
| 2 |
| 1 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
设f(x)=
,则f(f(
))=( )
|
| 10 |
| A、e | B、1 | C、2 | D、以上都不对 |
“3<a<4”是“函数f(x)=ax+3在(-1,2)上存在零点”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知a,b,c∈R,则“abc<0”是ax2+by2=c表示双曲线的 ( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
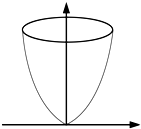 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是