题目内容
 某几何体如图所示,该几何体的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.该几何体的正视图和俯视图如图所示.
某几何体如图所示,该几何体的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.该几何体的正视图和俯视图如图所示.(1)请画出该几何体的侧视图,并标明线段长度;
(2)求该几何体的体积;
(3)求该几何体的侧面积.
考点:由三视图求面积、体积,棱柱、棱锥、棱台的侧面积和表面积
专题:计算题,作图题,空间位置关系与距离
分析:(1)由题意,侧视图如正视图相同,
(2)先求V长方体=40×40×20=32000;再求V正四棱锥=
×40×40×60=32000;求和即可;
(3)先求斜高h=
=20
;从而求侧面积.
(2)先求V长方体=40×40×20=32000;再求V正四棱锥=
| 1 |
| 3 |
(3)先求斜高h=
| 602+202 |
| 10 |
解答:
 解:(1)由题意,侧视图如正视图相同,如右图,
解:(1)由题意,侧视图如正视图相同,如右图,
(2)V长方体=40×40×20=32000;
V正四棱锥=
×40×40×60=32000;
故V=32000+32000=64000(cm3);
(3)斜高h=
=20
;
故侧面积为S=40×20×4+
×40×20
×4
=3200+1600
(cm2).
 解:(1)由题意,侧视图如正视图相同,如右图,
解:(1)由题意,侧视图如正视图相同,如右图,(2)V长方体=40×40×20=32000;
V正四棱锥=
| 1 |
| 3 |
故V=32000+32000=64000(cm3);
(3)斜高h=
| 602+202 |
| 10 |
故侧面积为S=40×20×4+
| 1 |
| 2 |
| 10 |
=3200+1600
| 10 |
点评:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
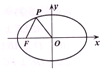 如图,已知椭圆C的中心为原点O,F(-2
如图,已知椭圆C的中心为原点O,F(-2| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|