题目内容
14.将函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{12}$个单位后的图象关于y轴对称,则函数f(x)在[0,$\frac{π}{2}$]上的最小值为-$\frac{\sqrt{3}}{2}$.分析 利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,求得f(x)的解析式,再根据正弦函数的定义域和值域,求得函数f(x)在[0,$\frac{π}{2}$]上的最小值.
解答 解:将函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{12}$个单位后,可得y=sin(2x-$\frac{π}{6}$+φ)的图象.
再根据所得图象关于y轴对称,可得-$\frac{π}{6}$+φ=kπ+$\frac{π}{2}$,求得φ=kπ+$\frac{2π}{3}$,k∈Z,故取φ=-$\frac{π}{3}$,f(x)=sin(2x-$\frac{π}{3}$).
∵x∈[0,$\frac{π}{2}$],∴2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],∴f(x)=sin(2x-$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],
则函数f(x)在[0,$\frac{π}{2}$]上的最小值为-$\frac{\sqrt{3}}{2}$,
故答案为:-$\frac{\sqrt{3}}{2}$.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
19.公差不为0的等差数列{an}的部分项an1,a${\;}_{{n}_{2}}$,a${\;}_{{n}_{3}}$,…构成等比数列{a${\;}_{{n}_{k}}$},且n2=2,n3=6,n4=22,则下列项中是数列{a${\;}_{{n}_{k}}$}中的项是( )
| A. | a46 | B. | a89 | C. | a342 | D. | a387 |
6.已知复数z=1+cosα+isinα(π<α<2π),则|$\overline{z}$|=( )
| A. | 2cos$\frac{α}{2}$ | B. | -2cos$\frac{α}{2}$ | C. | 2sin$\frac{α}{2}$ | D. | -2sin$\frac{α}{2}$ |
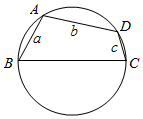 如图,设圆内接四边形ABCD的边BC为圆的直径,其余三边为a、b、c,求证:这个圆的直径是方程x3-(a2+b2+c2)x-2abc=0的根.
如图,设圆内接四边形ABCD的边BC为圆的直径,其余三边为a、b、c,求证:这个圆的直径是方程x3-(a2+b2+c2)x-2abc=0的根.