题目内容
19.公差不为0的等差数列{an}的部分项an1,a${\;}_{{n}_{2}}$,a${\;}_{{n}_{3}}$,…构成等比数列{a${\;}_{{n}_{k}}$},且n2=2,n3=6,n4=22,则下列项中是数列{a${\;}_{{n}_{k}}$}中的项是( )| A. | a46 | B. | a89 | C. | a342 | D. | a387 |
分析 由题意a2,a6,a22成等比数列,求出等比数列的公比q,
写出等比数列{${a}_{{n}_{k}}$}的通项公式,再验证选项是否正确即可.
解答 解:根据题意,等差数列{an}中,a2,a6,a22构成等比数列,
∴(a1+5d)2=(a1+d)(a1+21d),且d≠0,
解得d=3a1,
∴等比数列的公比为q=$\frac{{a}_{6}}{{a}_{2}}$=$\frac{{a}_{1}+5×{3a}_{1}}{{a}_{1}+{3a}_{1}}$=4;
又等差数列{an}的通项公式为
an=a1+(n-1)×3a1=3a1n-2a1=(3n-2)a1,
∴等比数列{${a}_{{n}_{k}}$}的通项公式为${a}_{{n}_{k}}$=a1•4n-1,
且a46=a1+45d=136a1,
a89=a1+88d=265a1,
a342=a1+341d=1024a1=a1•45,
a387=a1+386d=1159a1,
∴a342是数列{a${\;}_{{n}_{k}}$}中的项.
故选:C.
点评 本题考查了数列中某一项的判断问题,解题时要认真审题,注意等差数列和等比数列性质的合理运用.

练习册系列答案
相关题目
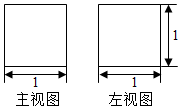 如图,某几何体的主视图与左视图都是边长为1的正方形,且其体积为$\frac{π}{4}$.则该几何体的俯视图可以是( )
如图,某几何体的主视图与左视图都是边长为1的正方形,且其体积为$\frac{π}{4}$.则该几何体的俯视图可以是( )