题目内容
7.已知底面为正三角形的直三棱柱内接于半径为1的球,当三棱柱的体积最大时,三棱柱的高为$\frac{{2\sqrt{3}}}{3}$.分析 画出图形,设O为外接球球心,三棱柱的高为h,表示出三棱柱的体积为$V=\frac{{3\sqrt{3}}}{16}(-{h^3}+4h)$,0<h<2.利用导数求解三棱柱的体积最大时,三棱柱的高.
解答 解:如图所示,设O为外接球球心,三棱柱的高为h,则由题意可知,A'O=B'O=C'O=1,$OE'=\frac{h}{2}$,$A'E'=\sqrt{1-\frac{h^2}{4}}$,$A'B'=\sqrt{3-\frac{{3{h^2}}}{4}}$,
此时三棱柱的体积为$V=\frac{{3\sqrt{3}}}{16}(-{h^3}+4h)$,其中0<h<2.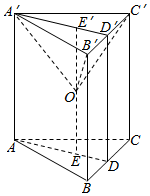
令y=-h3+4h(0<h<2),则y′=-3h2+4,令y′=0,
则$h=\frac{{2\sqrt{3}}}{3}$,当$0<h<\frac{{2\sqrt{3}}}{3}$时,y′>0,函数y增,
当$\frac{{2\sqrt{3}}}{3}<h<2$时,y′<0,函数y减.
故当三棱柱的体积最大时,三棱柱的高为$\frac{{2\sqrt{3}}}{3}$.
故答案为:$\frac{{2\sqrt{3}}}{3}$.
点评 本题考查几何体的体积的求法,导数的应用,考查转化思想以及计算能力空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.某三棱锥的正视图如图1所示,则在图2①②③④中,所有可能成为这个三棱锥的俯视图的是( )


| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
17.已知集合A={0,1,2},B={x|x(x-2)<0},则A∩B( )
| A. | {0,1,2} | B. | {1,2} | C. | {0,1} | D. | {1} |
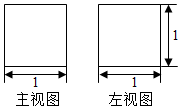 如图,某几何体的主视图与左视图都是边长为1的正方形,且其体积为$\frac{π}{4}$.则该几何体的俯视图可以是( )
如图,某几何体的主视图与左视图都是边长为1的正方形,且其体积为$\frac{π}{4}$.则该几何体的俯视图可以是( )