题目内容
已知一次函数f(x)=(m2-1)x+m2-3m+2,且f(1)=0.求:
(1)m的值;
(2)若f(x-1)≥x2,求x的取值范围.
(1)m的值;
(2)若f(x-1)≥x2,求x的取值范围.
考点:一元二次不等式的解法,函数的值
专题:不等式的解法及应用
分析:(1)由f(1)=0列出关于m的方程,求出m的值,需要验证函数是一次函数;
(2)由(1)求出函数的解析式,再化简f(x-1)≥x2,求出对应方程的判别式以及根,再求出不等式的解集.
(2)由(1)求出函数的解析式,再化简f(x-1)≥x2,求出对应方程的判别式以及根,再求出不等式的解集.
解答:
解:(1)由f(1)=0得,(m2-1)+m2-3m+2=0,
即2m2-3m+1=0,解得m=
或m=1,
当m=1时,f(x)不是一次函数,则m=
,
(2)由(1)得,f(x)=-
x+
,
所以f(x-1)≥x2化为:4x2+3x-6≤0,
则方程4x2+3x-6=0的判别式△=9-4×4×(-6)=105,
方程的根是x1=
,x2=
,
不等式4x2+3x-6≤0的解集是:[
,
].
即2m2-3m+1=0,解得m=
| 1 |
| 2 |
当m=1时,f(x)不是一次函数,则m=
| 1 |
| 2 |
(2)由(1)得,f(x)=-
| 3 |
| 4 |
| 3 |
| 4 |
所以f(x-1)≥x2化为:4x2+3x-6≤0,
则方程4x2+3x-6=0的判别式△=9-4×4×(-6)=105,
方程的根是x1=
-3-
| ||
| 8 |
-3+
| ||
| 8 |
不等式4x2+3x-6≤0的解集是:[
-3-
| ||
| 8 |
-3+
| ||
| 8 |
点评:本题考查待定系数法求函数的解析式,以及一元二次不等式的解法,考查了计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若3x=9,log2
=y,则x+2y等于( )
| 8 |
| 3 |
| A、6 |
| B、8-2log23 |
| C、4 |
| D、log48 |

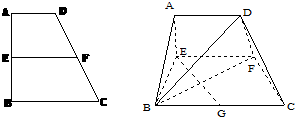 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=