题目内容
8.设函数f(x)=|x-a|+|x-5|,x∈R.(1)当a=2时,求不等式f(x)≥5的解集;
(2)已知a<5,若关于x的方程f(x)=ax有且只有两个实数解,求正实数a的取值范围.
分析 (1)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(2)由题意可得f(x)=$\left\{\begin{array}{l}{a+5-2x,x<a}\\{5-a,a≤x≤5}\\{2x-a-5,x>5}\end{array}\right.$的图象和直线y=ax有且只有两个交点,数形结合求得正实数a的取值范围.
解答 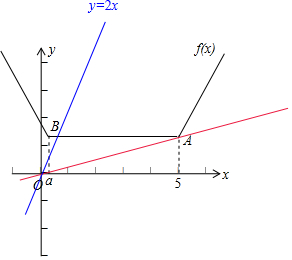 解:(1)当a=2时,f(x)=|x-a|+|x-5|=|x-2|+|x-5|,不等式f(x)≥5,等价于:
解:(1)当a=2时,f(x)=|x-a|+|x-5|=|x-2|+|x-5|,不等式f(x)≥5,等价于:
$\left\{\begin{array}{l}{x<2}\\{2-x+5-x≥5}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{2≤x≤5}\\{x-2+5-x≥5}\end{array}\right.$②,或 $\left\{\begin{array}{l}{x>5}\\{x-2+x-5≥5}\end{array}\right.$③.
解①求得x≤1,解②求得x∈∅,解③求得x≥6,
故原不等式的解集为{x|x≤1,或x≥6 }.
(2)已知a<5,若关于x的方程f(x)=$\left\{\begin{array}{l}{a+5-2x,x<a}\\{5-a,a≤x≤5}\\{2x-a-5,x>5}\end{array}\right.$=ax有且只有两个实数解,
即函数f(x)的图象和直线y=ax有且只有两个交点,
结合函数f(x)的图象,点A(5,5-a),B(a,5-a),
直线OA的斜率为KOA=$\frac{5-a}{5}$,图中蓝色的直线方程为y=2x,和f(x)右端的射线平行,
∴$\frac{5-a}{5}$<a<2,求得$\frac{5}{6}$<a<2.
点评 本题主要考查绝对值不等式的求法,带有绝对值的函数,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $-\frac{\sqrt{3}}{2}$ |

| A. | 22 | B. | 25 | C. | 28 | D. | 31 |
| A. | 函数g(x)是奇函数 | B. | 函数g(x)在区间[π,2π]上是增函数 | ||
| C. | 函数g(x)的最小正周期是4π | D. | 函数g(x)的图象关于直线x=π对称 |
| A. | ?x>0,总有2x≤1 | B. | ?x≤0,总有2x≤1 | C. | ?x≤0,使得2x≤1 | D. | ?x>0,使得2x≤1 |
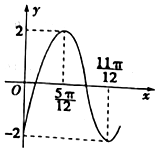 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.