题目内容
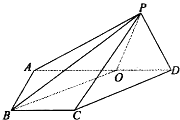如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA⊥PD，底面ABCD是直角梯形，其中BC∥AD，∠BAD=90°，AD=3BC，O是AD上一点．（Ⅰ）若AD=3OD，求证：CD∥平面PBO；
（Ⅱ）求证：平面PAB⊥平面PCD．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（Ⅰ）由AD=3BC，AD=3OD，推断出OD=BC，又OD∥BC，可知四边形BCDO为平行四边形，推断出CD∥BO，根据线面平行的判定定理证明出CD∥平面PBO．
（Ⅱ）由侧面PAD⊥底面ABCD，AB?底面ABCD，AB⊥AD，推断出AB⊥平面PAD，根据线面垂直的性质知AB⊥PD，进而根据线面垂直的判定定理可知PD⊥平面PAB，进而根据面面垂直的判定定理推断出平面PAB⊥平面PCD．
（Ⅱ）由侧面PAD⊥底面ABCD，AB?底面ABCD，AB⊥AD，推断出AB⊥平面PAD，根据线面垂直的性质知AB⊥PD，进而根据线面垂直的判定定理可知PD⊥平面PAB，进而根据面面垂直的判定定理推断出平面PAB⊥平面PCD．
解答：
证明：（Ⅰ）∵AD=3BC，AD=3OD，
∴OD=BC，
∵OD∥BC，
∴四边形BCDO为平行四边形，
∴CD∥BO，又BO?平面PBO，CD?平面PBO，
∴CD∥平面PBO．
（Ⅱ）∵侧面PAD⊥底面ABCD，AB?底面ABCD，AB⊥AD，
∴AB⊥平面PAD，
∵PD?平面PAD，
∴AB⊥PD，
又PA⊥PD，且PA?平面PAB，AB?平面PAB，AB∩PA=A，
∴PD⊥平面PAB，
∵PD?平面PCD，
∴平面PAB⊥平面PCD．
∴OD=BC，
∵OD∥BC，
∴四边形BCDO为平行四边形，
∴CD∥BO，又BO?平面PBO，CD?平面PBO，
∴CD∥平面PBO．
（Ⅱ）∵侧面PAD⊥底面ABCD，AB?底面ABCD，AB⊥AD，
∴AB⊥平面PAD，
∵PD?平面PAD，
∴AB⊥PD，
又PA⊥PD，且PA?平面PAB，AB?平面PAB，AB∩PA=A，
∴PD⊥平面PAB，
∵PD?平面PCD，
∴平面PAB⊥平面PCD．
点评：本题主要考查了线面垂直，面面垂直的判定定理及性质．证明面面垂直的关键是找到平面中与另一平面垂直的直线．
练习册系列答案
相关题目
如图，四边形ABCD是边长为2的正方形，△ABE为等腰三角形，AE=BE，平面ABCD⊥平面ABE，动点F在CE上，无论点F运动到何处时，总有BF⊥AE．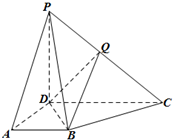
在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，底面ABCD是直角梯形，AB∥CD，∠ADC=