题目内容
已知函数f(x)=loga(x+1)-loga(1-x),a>0且a≠1
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明;
(3)当a>1时,求使f(x)<0成立的x的取值范围.
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明;
(3)当a>1时,求使f(x)<0成立的x的取值范围.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)由函数解析式可得可得
,由此求得函数的定义域.
(2)由f(x)的定义域关于原点对称,f(-x)=-f(x),可得函数为偶函数.
(3)由题意可得 0<
<1,即
,由此解得x的范围.
|
(2)由f(x)的定义域关于原点对称,f(-x)=-f(x),可得函数为偶函数.
(3)由题意可得 0<
| 1+x |
| 1-x |
|
解答:
解:(1)由函数f(x)=loga(x+1)-loga(1-x),a>0且a≠1,
可得
,解得-1<x<1,故函数的定义域为(-1,1).
(2)由f(x)=loga
,且定义域关于原点对称,
f(-x)=loga
=-loga
=-f(x),故函数为奇函数.
(3)当a>1时,由f(x)<0可得 0<
<1,即
,
即
,解得-1<x<0.
可得
|
(2)由f(x)=loga
| 1+x |
| 1-x |
f(-x)=loga
| 1-x |
| 1+x |
| 1+x |
| 1-x |
(3)当a>1时,由f(x)<0可得 0<
| 1+x |
| 1-x |
|
即
|
点评:本题主要考查对数函数的图象和性质综合应用,体现了等价转化的数学思想,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
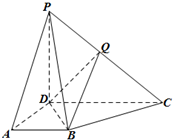 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=