题目内容
已知某一种物质每100年其质量就减少10%．设其物质质量为m，则过x年后，其物质的质量y与x的函数关系式为（ ）
| A、y=0.9100xm | ||
B、y=0.9
| ||
C、（1-0.1
| ||
| D、y=（1-0.1100x）m |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：利用函数的增长率模型，是指数函数类型，进行解答即可．
解答：
解：∵该种物质每100年其质量减少10%，
设其物质质量为m时，
∴过x年后，该种物质的质量y与x的函数关系式为
y=m•(1-10%)
=m•0.9
=0.9
m．
故选：B．
设其物质质量为m时，
∴过x年后，该种物质的质量y与x的函数关系式为
y=m•(1-10%)
| x |
| 100 |
| x |
| 100 |
| x |
| 100 |
故选：B．
点评：本题考查了函数的增长率的应用问题，是指数函数模型的应用问题，是基础题目．
练习册系列答案
教材全解字词句篇系列答案
相关题目
已知m、n表示两条不同直线，α表示平面．下列四个命题中，正确的个数是（ ）
①若m∥α，n∥α，则m∥n②若m⊥α，n?α，则m⊥n
③若m⊥α，m⊥n，则n∥α④若m∥α，m⊥n，则n⊥α
①若m∥α，n∥α，则m∥n②若m⊥α，n?α，则m⊥n
③若m⊥α，m⊥n，则n∥α④若m∥α，m⊥n，则n⊥α
| A、4 | B、3 | C、2 | D、1 |
若m，n是两条不同的直线，α，β，γ是两个不同的平面，则下列命题中的真命题是（ ）
| A、若m?β，α⊥β，则m⊥α |
| B、若α∥β，m?α，n?β则m∥n |
| C、若m⊥β，m∥α，则α⊥β |
| D、若m∥n，n?α，则m∥α |
函数f（x）=
+
的定义域是（ ）
| 3x2 | ||
|
| 3x+1 |
A、（-
| ||
B、（-
| ||
C、[-
| ||
| D、[0，1） |
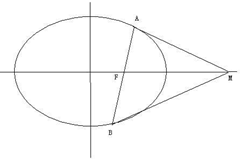如图，椭圆