题目内容
要得到函数y=sin(2x-
),x∈R的图象,只需将函数y=sin2x,x∈R图象上所有的点( )
| π |
| 3 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:把函数y=sin(2x-
)变形为y=sin2(x-
),则答案可求.
| π |
| 3 |
| π |
| 6 |
解答:
解:∵y=sin(2x-
)=sin2(x-
),
∴要得到函数y=sin(2x-
),x∈R的图象,只需将函数y=sin2x,x∈R图象上所有的点向右平行移动
个单位长度.
故选:B.
| π |
| 3 |
| π |
| 6 |
∴要得到函数y=sin(2x-
| π |
| 3 |
| π |
| 6 |
故选:B.
点评:本题主要考查三角函数的平移.三角函数的平移原则为左加右减上加下减,是基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知平面向量
=(sinα,
),
=(1,1)且
∥
,则锐角α的值为( )
| a |
| 1 |
| 2 |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)为定义在R上的奇函数,且在(0,+∞)内是增函数,又f(2)=0,则不等式xf(x)<0的解集为( )
| A、(-2,0)∪(2,+∞) |
| B、(-∞,-2)∪(0,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-2,0)∪(0,2) |
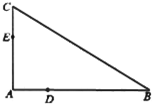 如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x-mn=0的两个根.
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x-mn=0的两个根. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.