题目内容
15.若圆${C_1}:{(x-1)^2}+{y^2}=1$与圆${C_2}:{x^2}+{y^2}-8x-8y+m=0$相交,则m的取值范围为( )| A. | (-2,8) | B. | (-∞,-2)∪(8,+∞) | C. | (-4,16) | D. | (-∞,-4)∪(16,+∞) |
分析 由题意得到圆C1的圆心和半径,化圆的一般方程为标准方程,求出圆C2的圆心与半径,由两圆圆心距间的关系与半径间关系列关于m的不等式得答案.
解答 解:圆${C_1}:{(x-1)^2}+{y^2}=1$的圆心坐标C1(1,0),半径r1=1,
由${C_2}:{x^2}+{y^2}-8x-8y+m=0$,得(x-4)2+(y-4)2=32-m,
∴圆C2的圆心坐标(4,4),半径${r}_{2}=\sqrt{32-m}$.
则${|C}_{1}{C}_{2}|=\sqrt{(4-1)^{2}+(4-0)^{2}}=5$,
∵圆${C_1}:{(x-1)^2}+{y^2}=1$与圆${C_2}:{x^2}+{y^2}-8x-8y+m=0$相交,
∴$\sqrt{32-m}-1<5<\sqrt{32-m}+1$,解得-4<m<16.
∴m的取值范围为(-4,16).
故选:C.
点评 本题考查圆与圆的位置关系,关键是熟练掌握两圆圆心距间的关系与半径间关系的应用,是中档题.

练习册系列答案
相关题目
3.某种计算机病毒是通过电子邮件进行传播的,表格是某公司前5天监测到的数据:
则下列函数模型中能较好地反映在第x天被感染的数量y与x之间的关系的是( )
| 第x天 | 1 | 2 | 3 | 4 | 5 |
| 被感染的计算机数量y(台) | 12 | 24 | 49 | 95 | 190 |
| A. | y=12x | B. | y=6x2-6x+12 | C. | y=6•2x | D. | y=12log2x+12 |
20.执行如图所示的程序框图,若输入S的值为$\frac{1}{2}$,则输出S的值为( )
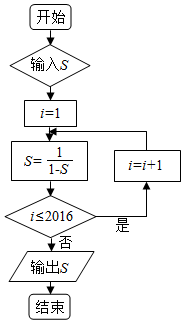

| A. | -1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
7.函数f(x)=$\left\{\begin{array}{l}{\sqrt{2-|x-2|},}&{x∈[0,4]}\\{\frac{1}{2}f(x-4),}&{x∈(4,+∞)}\end{array}\right.$,若x>0时,不等式f(x)≤$\frac{m}{x}$恒成立,则实数m的取值范围为( )
| A. | [4$\sqrt{2}$,+∞) | B. | [3$\sqrt{2}$,+∞) | C. | [2$\sqrt{2}$,+∞) | D. | [$\frac{5}{2}$$\sqrt{2}$,+∞) |
4.某班级举行一次“科普知识”竞赛活动,活动分为初赛和决赛两个阶段.现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表:
(Ⅰ)填写频率分布表中的空格;
(Ⅱ)决赛规则如下:参加决赛的每位同学从给定的5道小题中依次口答,答对3道题就终止答题并获一等奖;如果前3道题都答错就不再答第4、5题而被淘汰.某同学进入决赛,每道题答对的概率均为0.5.
①求该同学恰好答满5道题并获一等奖的概率;
②记该同学决赛中答题的个数为X,求X的分布列及数学期望.
| 分 组(分数段) | 频 数(人 数) | 频 率 |
| [60,70) | 8 | |
| [70,80) | 0.44 | |
| [80,90) | 14 | 0.28 |
| [90,100 | ||
| 合 计 | 50 | 1 |
(Ⅱ)决赛规则如下:参加决赛的每位同学从给定的5道小题中依次口答,答对3道题就终止答题并获一等奖;如果前3道题都答错就不再答第4、5题而被淘汰.某同学进入决赛,每道题答对的概率均为0.5.
①求该同学恰好答满5道题并获一等奖的概率;
②记该同学决赛中答题的个数为X,求X的分布列及数学期望.
 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的两个顶点恰好是双曲线y2-x2=1的两个焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的两个顶点恰好是双曲线y2-x2=1的两个焦点. 如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出.坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米的造价为60万元.
如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出.坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米的造价为60万元.