Question

1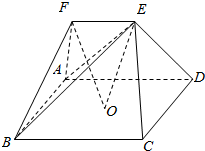．如图，在五面体ABCDEF中，点O是矩形ABCD的对角线的交点，△ABF是等边三角形，棱EF∥BC，且EF=$\frac{1}{2}$BC．
（1）证明：EO∥平面ABF；
（2）若有OF⊥平面ABE，试求$\frac{BC}{CD}$的值．

Answer 1

分析 （1）通过证平行四边形证线线平行，再由线线平行证明线面平行即可；
（2）若有OF⊥平面ABE，则OF⊥EM，四边形EFMO为菱形，进而得到答案．本题考查的知识点是直线与平面平行的判定，直线与平面垂直的性质，难度中档．

解答 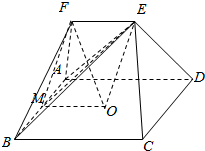证明：（1）证明：取AB的中点M，连接FM，OM，

∵O为矩形ABCD的对角线的交点，
∴OM∥BC，且OM=$\frac{1}{2}$BC，
又EF∥BC，且EF=$\frac{1}{2}$BC，
∴OM=EF，且EF∥OM，
∴四边形EFMO为平行四边形，
∴EO∥FM，
又∵FM?平面ABF，EO?平面ABF，
∴EO∥平面ABF．
（2）∵OF⊥平面ABE，EM?平面ABE，
∴OF⊥EM，
则四边形EFMO为菱形，
则FM=OM=$\frac{1}{2}$BC，
又∵△ABF是等边三角形，
∴FM=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$CD，
故$\frac{BC}{CD}$=$\sqrt{3}$．

点评 本题考查的知识点是直线与平面平行的判定，直线与平面垂直的性质，难度中档．