题目内容
9.设函数f(x)=|2x-1|+3x-4,记不等式f(x)<-3的解集为M.(Ⅰ)求M;
(Ⅱ)当x∈M时,证明:x[f(x)]2-x2|f(x)|<0.
分析 (Ⅰ)分类讨论,即可求M;
(Ⅱ)当x∈M时,要证x[f(x)]2-x2|f(x)|<0,只需证[f(x)]2-x|f(x)|>0.
解答 (Ⅰ)解:依题设,当x$≤\frac{1}{2}$时,由f(x)=x-3<-3,解得x<0,此时x<0,;
当x>$\frac{1}{2}$时,由f(x)=5x-5<-3,解得x$<\frac{2}{5}$,此时x∈∅.
∴f(x)<-3的解集为M=(-∞,0).
(Ⅱ)证明:当x∈M时,要证x[f(x)]2-x2|f(x)|<0,
只需证[f(x)]2-x|f(x)|>0,
由(Ⅰ)知,当x∈M时,f(x)=x-3,
∴[f(x)]2-x|f(x)|=(x-3)(2x-3),
又∵x-3<0,2x-3<0,∴[f(x)]2-x|f(x)|>0,
∴x[f(x)]2-x2|f(x)|<0.
点评 本题考查不等式的解法,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.函数y=2sin2(x+$\frac{3π}{2}$)-1是( )
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为$\frac{π}{2}$的奇函数 |
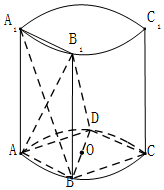 如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.
如图,在圆柱中,A,B,C,D是底面圆的四等分点,O是圆心,A1A,B1B,C1C与底面ABCD垂直,底面圆的直径等于圆柱的高.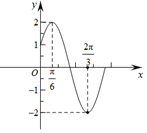 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.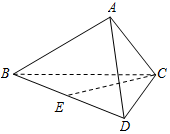 如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.
如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.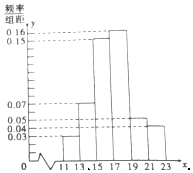 一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.
一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.