题目内容
1.在平面直角坐标系xOy中,已知角α的顶点和点O重合,始边与x轴的非负半轴重合,终边上一点M坐标为(-1,$\sqrt{3}$),则tan(α+$\frac{π}{4}$)=$\sqrt{3}-2$.分析 根据三角函数的定义求解tanα的值,利用和与差公式即可求解tan(α+$\frac{π}{4}$)的值.
解答 解:由题意,根据三角函数的定义,tanα=$\frac{y}{x}$=$-\sqrt{3}$.
那么:tan(α+$\frac{π}{4}$)=$\frac{tanα+tan\frac{π}{4}}{1-tanαtan\frac{π}{4}}$=$\frac{-\sqrt{3}+1}{1+\sqrt{3}}$=$\sqrt{3}-2$
故答案为:$\sqrt{3}-2$.
点评 本题考查了三角函数的定义的运用和正切的和与差的公式的计算.属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
11.已知数列{an}为等比数列,且a2013+a2015=$\int_0^2{\sqrt{4-{x^2}}}$dx,则a2014(a2012+2a2014+a2016)的值为( )
| A. | π2 | B. | 4π2 | C. | π | D. | 2π |
12.甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于95为正品,小于95为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
(1)试分别估计甲机床、乙机床生产的零件为正品的概率;
(2)甲机床生产一件零件,若是正品可盈利160元,次品则亏损20元;乙机床生产一件零件,若是正品可盈利200元,次品则亏损40元,在(1)的前提下,现需生产这种零件2件,以获得利润的期望值为决策依据,应该如何安排生产最佳?
| 测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
| 机床甲 | 8 | 12 | 40 | 32 | 8 |
| 机床乙 | 7 | 18 | 40 | 29 | 6 |
(2)甲机床生产一件零件,若是正品可盈利160元,次品则亏损20元;乙机床生产一件零件,若是正品可盈利200元,次品则亏损40元,在(1)的前提下,现需生产这种零件2件,以获得利润的期望值为决策依据,应该如何安排生产最佳?
10.设复数z满足$\frac{{{{({1+i})}^2}}}{z}=1-i$,则z=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
11.已知定义在R上的奇函数f(x)满足f(1)=e(e为自然对数的底数),且当x≥0时,有(x-1)f(x)<xf'(x),则不等式xf(x)-e|x|>0的解集是( )
| A. | (-∞,-1)∪(1,+∞) | B. | (-1,0)∪(0,1) | C. | (-1,1) | D. | (-1,0)∪(1,+∞) |
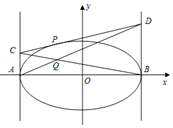 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.