题目内容
2.如果数列{an}中任意连续三项奇数项与连续三项偶数项均能构成一个三角形的边长,则称{an}为“亚三角形”数列;对于“亚三角形”数列{an},如果函数使得y=f(x)仍为一个“亚三角形”数列,则称y=f(x)是数列{an}的一个“保亚三角形函数”(n∈N*).记数列{an}的前项和为Sn,c1=2016,且5Sn+1-4Sn=10080,若g(x)=lgx是数列{cn}的“保亚三角形函数”,则数列{cn}的项数的最大值为( )(参考数据:lg2≈0.30,lg2016≈3.304}.| A. | 33 | B. | 34 | C. | 35 | D. | 36 |
分析 先利用条件求出数列{cn}的通项公式,证明其满足“亚三角形”数列.然后利用对数型复合函数的单调性得到g(cn)是单调递减函数,再由lgcn+4+lgcn+2>lgcn求解对数不等式得答案.
解答 解:由5Sn+1-4Sn=10080,得
5Sn-4Sn-1=10080(n≥2),两式作差得:5cn+1-4cn=0(n≥2).
∴$\frac{{c}_{n+1}}{{c}_{n}}=\frac{4}{5}$(n≥2).
又c1=2016,且5Sn+1-4Sn=10080,
∴5(c1+c2)-4c1=10080,解得,${c}_{2}=\frac{8064}{5}$.
∴$\frac{{c}_{2}}{{c}_{1}}=\frac{\frac{8064}{5}}{2016}=\frac{4}{5}$.
则数列{cn}是等比数列.
∴${c}_{n}=2016•(\frac{4}{5})^{n-1}$.
由上可知,数列{cn}是递减数列.
∵${c}_{n+4}+{c}_{n+2}=2016•(\frac{4}{5})^{n+3}+2016•(\frac{4}{5})^{n+1}$=$\frac{656}{625}•2016•(\frac{4}{5})^{n-1}>2016•(\frac{4}{5})^{n-1}={c}_{n}$.
∴数列{cn}是“亚三角形”数列;
函数g(x)=lgx是增函数,则lgcn是减函数.
由lgcn+4+lgcn+2>lgcn得,$lg2016+(n+3)lg\frac{4}{5}+lg2016+(n+1)lg\frac{4}{5}$$>lg2016+(n-1)lg\frac{4}{5}$.
整理得:$(n+5)lg\frac{4}{5}>-lg2016$.
解得:n<33.04.
则数列{cn}的项数的最大值为33.
故选:A.
点评 本题是在新定义下对数列的综合考查,考查了对数函数的单调性.关于新定义的题型,在作题过程中一定要理解定义,并会用定义来解题,是中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
| A. | $\sqrt{2}$-1 | B. | 2-$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | y=±$\frac{2}{3}$x | B. | y=±$\frac{4}{9}$x | C. | y=±$\frac{3}{2}$x | D. | y=±$\frac{9}{4}$x |
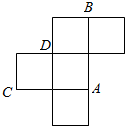 如图是一个无盖的正方体盒子展开后的平面图,A,B,C,D是展开图上的四点,则在正方体盒子中,直线AB与CD的位置关系是异面,∠ABC的值为60°.
如图是一个无盖的正方体盒子展开后的平面图,A,B,C,D是展开图上的四点,则在正方体盒子中,直线AB与CD的位置关系是异面,∠ABC的值为60°.