题目内容
14．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点和左焦点分别为A、F，O为坐标原点，点H的坐标为H（-$\frac{{a}^{2}}{c}$，0），若$\overrightarrow{AF}$=λ$\overrightarrow{OH}$，则实数λ的值可能是（ ）| A． | $\sqrt{2}$-1 | B． | 2-$\sqrt{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
分析 利用$\overrightarrow{AF}$=λ$\overrightarrow{OH}$，可得（a-c，0）=λ（$\frac{{a}^{2}}{c}$，0），求出λ的范围，即可得出结论．
解答 解：∵$\overrightarrow{AF}$=λ$\overrightarrow{OH}$，
∴（a-c，0）=λ（$\frac{{a}^{2}}{c}$，0），
∴λ=$\frac{ac-{c}^{2}}{{a}^{2}}$=e-e2=e（1-e）＜0，
故选：A
点评 本题考查双曲线的方程与性质，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
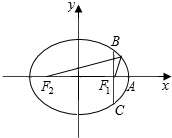电影放映机上聚光灯泡的反射面，是由椭圆的一部分CAB（如图），绕着OA轴旋转而成的，如果把灯泡放在椭圆的一个焦点F1处，那么根据椭圆的光学性质，由F1发出光线，经反射面反射后，都集中在椭圆的另一个焦点F2处，因此，只要把影片放在F2处，就可以得到最强的光线，现已知|F1A|=1.5cm，|BC|=5.2cm，那么聚光灯泡F1与影片门F2之间应该距离多少cm．