题目内容

11．双曲线$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=1的渐近线方程是（　　）
A．y=±$\frac{2}{3}$xB．y=±$\frac{4}{9}$xC．y=±$\frac{3}{2}$xD．y=±$\frac{9}{4}$x

分析 直接根据双曲线的方程，令方程的右边等于0求出渐近线的方程．

解答 解：已知双曲线$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=1
令：$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=0
即得到渐近线方程为：y=±$\frac{2}{3}$x
故选：A．

点评 本题考查的知识要点：双曲线的渐渐线方程的求法，比较基础．

练习册系列答案
相关题目
1．已知函数f（x）=x3-x2+x+1，
（1）求函数在点（1，2）处的切线
（2）求函数在点（1，2）处的切线与函数g（x）=x2围成的图形的面积．
2．如果数列{an}中任意连续三项奇数项与连续三项偶数项均能构成一个三角形的边长，则称{an}为“亚三角形”数列；对于“亚三角形”数列{an}，如果函数使得y=f（x）仍为一个“亚三角形”数列，则称y=f（x）是数列{an}的一个“保亚三角形函数”（n∈N*）．记数列{an}的前项和为Sn，c1=2016，且5Sn+1-4Sn=10080，若g（x）=lgx是数列{cn}的“保亚三角形函数”，则数列{cn}的项数的最大值为（　　）（参考数据：lg2≈0.30，lg2016≈3.304}．
A．33B．34C．35D．36
19．焦点为（0，±3）且与双曲线$\frac{x^2}{2}$-y2=1有相同的渐近线的双曲线方程是$\frac{{y}^{2}}{3}$-$\frac{{x}^{2}}{6}$=1．
6．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1、F2，离心率为$\frac{\sqrt{3}}{3}$，点M在椭圆上，且满足MF1⊥x轴，|MF1|=$\frac{4\sqrt{3}}{3}$．
（1）求椭圆的方程；
（2）若直线y=kx+2交椭圆于A、B两点，求△ABO（O为坐标原点）面积的最大值．
16．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;（a＞b＞0）$，短轴顶点B（0，b），若椭圆内接三角形BMN的重心是椭圆的左焦点F，求椭圆的离心率的取值范围．
3．已知a∈R，函数f（x）=x2-2ax+5
（1）若不等式f（x）＞0对任意x∈（0，+∞）恒成立，求实数a的取值范围；
（2）若a＞1，且函数f（x）的定义域和值域均为[1，a]，求实数a的值．
20．已知点P是函数y=sin（x+θ）图象与x轴的一个交点，A，B为P点右侧同一周期上的最大和最小值点，则$\overrightarrow{PA}•\overrightarrow{PB}$=（　　）
A．$\frac{{\sqrt{3}{π^2}}}{4}-1$B．$\frac{{3{π^2}}}{4}-1$C．$\frac{{3{π^2}}}{2}-1$D．$\frac{π^2}{2}-1$
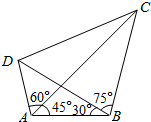1．如图，在平面四边形ABCD中，AB=5$\sqrt{2}$，∠CBD=75°，∠ABD=30°，∠CAB=45°，∠CAD=60°．
（1）求△ABC的面积S△ABC；
（2）求CD的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网