题目内容
7.已知A(-2,0),B(2,0),且△ABC的周长为12,求点C的轨迹方程.分析 由△ABC的周长及AB的长,得|CA|+|CB|,由圆锥曲线的定义可判断轨迹的形状,即可得其方程.
解答 解:由题意知,|CA|+|CB|=12-|AB|=8>|AB|,
故动点C在椭圆上,
当C与A,B共线时,A,B,C三点不能围成三角形,
故轨迹E不含x轴上的两点,
由于定点A,B在x轴上,
可设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
则2a=8,焦距2c=4,从而b2=a2-c2=12,
即得C的轨迹方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1(y≠0).
点评 本题考查轨迹方程的求法,注意运用椭圆的定义,以及方程的等价性,属于基础题和易错题.

练习册系列答案
相关题目
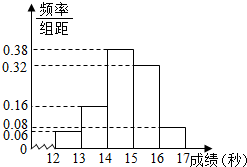 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.