题目内容
17.已知tanα=-$\frac{1}{3}$,α∈($\frac{3π}{2}$,2π),求sin2α,cos2α,tan2α的值.分析 利用二倍角公式,写成关于tanα的形式,代入求值.
解答 解:α∈($\frac{3π}{2}$,2π),2α∈(3π,4π),
sin2α=$\frac{2tanα}{1+ta{n}^{2}α}$=$\frac{2×(-\frac{1}{3})}{1+(-\frac{1}{3})^{2}}$=$-\frac{3}{5}$,
cos2α=$\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$=$\frac{4}{5}$,
tan2α=$\frac{2ta{n}^{2}α}{1-ta{n}^{2}α}$=-$\frac{3}{4}$.
点评 本题考查正弦余弦正切函数的二倍角公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.如图在平行四边形ABCD中,E、F分别是AB、BC边中点,线段CE、DF相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AG}$=( )
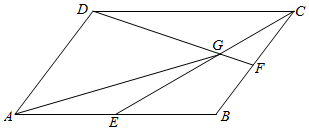

| A. | $\frac{4}{5}$$\overrightarrow{a}$+$\frac{3}{5}$$\overrightarrow{b}$ | B. | $\frac{3}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | C. | $\frac{5}{6}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{5}{6}$$\overrightarrow{b}$ |