题目内容
10.已知数列{an}满足a1=1,a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n}$an=an+1-1(n∈N),数列{an}的前n项和为Sn.(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{S}_{n}}$,Tn是数列{bn}的前n项和,求使得Tn<$\frac{m}{10}$对所有n∈N,都成立的最小正整数m.
分析 (1)通过a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1+$\frac{1}{n}$an=an+1-1与a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1=an-1作差,进而计算可知$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$(n∈N),利用累乘法计算可知数列{an}的通项公式;
(2)通过(1),利用等差数列的求和公式裂项可知bn=2($\frac{1}{n}$-$\frac{1}{n+1}$),进而利用并项相消法可知Tn=$\frac{2n}{n+1}$,从而问题转化为数列{Tn}的最大值,计算即得结论.
解答 解:(1)∵a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1+$\frac{1}{n}$an=an+1-1(n∈N),
∴当n≥2时,a1+$\frac{1}{2}$a2+$\frac{1}{3}$a3+…+$\frac{1}{n-1}$an-1=an-1,
两式相减得:$\frac{1}{n}$an=an+1-an,即$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,
又∵$\frac{{a}_{2}}{{a}_{1}}$=$\frac{1+{a}_{1}}{{a}_{1}}$=$\frac{2}{1}$满足上式,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$(n∈N),
∴当n≥2时,an=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$•…•$\frac{{a}_{2}}{{a}_{1}}$•a1
=$\frac{n}{n-1}$•$\frac{n-1}{n-2}$•…•2•1
=n,
又∵a1=1满足上式,
∴数列{an}的通项公式an=n;
(2)由(1)可知bn=$\frac{1}{{S}_{n}}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),
∴Tn=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$,
∵$\frac{2n}{n+1}$随着n的增大而增大,
∴不等式Tn<$\frac{m}{10}$对所有n∈N都成立?求数列{Tn}的最大值,
又∵$\underset{lim}{n→∞}$$\frac{2n}{n+1}$=2,
∴$\frac{m}{10}$≥2,即m≥20,
故满足题意的最小正整数m=20.
点评 本题考查数列的通项及前n项和,考查累乘法,考查裂项相消法,注意解题方法的积累,属于中档题.

| A. | {-1,0} | B. | {-1,0,1} | C. | {-2,-1,0} | D. | {-2,-1,1} |
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
| A. | 若|m-3|≤2则m<5或m>1 | B. | 若|m-3|≤2则m≤5或m≥1 | ||
| C. | 若|m-3|>2则1<m<5 | D. | 若|m-3|>2则1≤m≤5 |
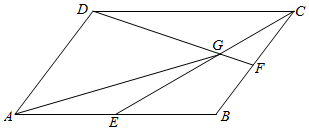
| A. | $\frac{4}{5}$$\overrightarrow{a}$+$\frac{3}{5}$$\overrightarrow{b}$ | B. | $\frac{3}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | C. | $\frac{5}{6}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{5}{6}$$\overrightarrow{b}$ |