题目内容
若函数f(x)=22x+2xa+a+1.
(1)求函数f(x)的值域;
(2)若f(x)>-3对任意的x∈[0,2]恒成立,求a的取值范围;
(3)讨论f(x)的零点的个数.
(1)求函数f(x)的值域;
(2)若f(x)>-3对任意的x∈[0,2]恒成立,求a的取值范围;
(3)讨论f(x)的零点的个数.
考点:指数型复合函数的性质及应用,函数恒成立问题,函数零点的判定定理
专题:函数的性质及应用
分析:(1)令t=2x>0,可得f(x)=g(t)=t2+at+a+1=(t+
)2+a+1-
,再利用二次函数的性质分类讨论求得g(t)在(0,+∞)上的值域.
(2)由题意可得f(x)在[0,2]上的最小值大于-3,即g(t)在[1,4]上的最小值大于-3.再利用二次函数的性质分类讨论求得g(t)在(0,+∞)上的最小值,即可求得a的范围.
(3)f(x)的零点的个数,即函数g(t)=t2+at+a+1在(0,+∞)上的零点个数.再利用二次函数的性质分类讨论,得出结论.
| a |
| 2 |
| a2 |
| 4 |
(2)由题意可得f(x)在[0,2]上的最小值大于-3,即g(t)在[1,4]上的最小值大于-3.再利用二次函数的性质分类讨论求得g(t)在(0,+∞)上的最小值,即可求得a的范围.
(3)f(x)的零点的个数,即函数g(t)=t2+at+a+1在(0,+∞)上的零点个数.再利用二次函数的性质分类讨论,得出结论.
解答:
解:(1)令t=2x>0,可得f(x)=g(t)=t2+at+a+1=(t+
)2+a+1-
,
当a≥0时,-
≤0,二次函数g(t)的图象的对称轴方程为t=-
,函数g(t)在(0,+∞)上单调递增,g(t)>g(0)=a+1,
故函数的值域为(a+1,+∞).
当a<0时,二次函数g(t)的图象的对称轴方程为t=-
>0,函数g(t)的最小值为g(-
)=a+1-
,
故函数的值域为[a+1-
,+∞).
(2)若f(x)>-3对任意的x∈[0,2]恒成立,则f(x)在[0,2]上的最小值大于-3,
即g(t)在[1,4]上的最小值大于-3.
①当a≥0时,由于g(t)在[1,4]上单调递增,故g(t)的最小值为g(1)=2a+2,由2a+2>-3,求得a>-
,
综合可得当a≥0.
②当-2≤a<0,二次函数g(t)的图象的对称轴方程为t=-
(0,1],g(t)在[1,4]上单调递增,
函数g(t)的最小值为g(1)=2a+2,由2+2a>-3,求得a>-
,
综合可得-2≤a<0.
③当-8<a<-2时,二次函数g(t)的图象的对称轴方程为t=-
∈(1,4),g(t)的最小值为g(-
)=a+1-
,
由a+1-
>-3,求得2-2
<a<2+2
,综合可得2-2
<a<-2.
④当a≤-8,二次函数g(t)的图象的对称轴方程为t=-
≥4,g(t)在[1,4]上单调递减,
g(t)的最小值为g(4)=5a+17,由5a+17>-3,求得a>-4,不满足前提条件a≤-8,故舍去.
综合①②③④可得,a≥2-2
.
(3)f(x)的零点的个数,即函数g(t)=t2+at+a+1在(0,+∞)上的零点个数.
①当△=a2-4(a+1)<0时,即2-2
<a<2+2
时,函数g(t)在(0,+∞)上的零点个数为0.
②当a=2-2
或a=2+2
时,△=0,再根据二次函数g(t)的图象的对称轴方程为t=-
,
可得当a=2-2
时,t=-
>0,函数g(t)在(0,+∞)上有唯一零点;当a=2+2
时,t=-
<0,函数g(t)在(0,+∞)上没有零点.
③当a<2-2
时,△>0,由t=-
>0,g(0)=a+1>0,可得函数g(t)在(0,+∞)上有2个零点;
当a>2+2
时,△>0,由t=-
<0,g(0)=a+1>0,可得函数g(t)在(0,+∞)上没有零点.
综上可得,a>2-2
时,函数g(t)在(0,+∞)上的零点个数为0;
当a=2-2
时,函数g(t)在(0,+∞)上有唯一零点;
当a<2-2
时,函数g(t)在(0,+∞)上有2个零点.
| a |
| 2 |
| a2 |
| 4 |
当a≥0时,-
| a |
| 2 |
| a |
| 2 |
故函数的值域为(a+1,+∞).
当a<0时,二次函数g(t)的图象的对称轴方程为t=-
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
故函数的值域为[a+1-
| a2 |
| 4 |
(2)若f(x)>-3对任意的x∈[0,2]恒成立,则f(x)在[0,2]上的最小值大于-3,
即g(t)在[1,4]上的最小值大于-3.
①当a≥0时,由于g(t)在[1,4]上单调递增,故g(t)的最小值为g(1)=2a+2,由2a+2>-3,求得a>-
| 5 |
| 2 |
综合可得当a≥0.
②当-2≤a<0,二次函数g(t)的图象的对称轴方程为t=-
| a |
| 2 |
函数g(t)的最小值为g(1)=2a+2,由2+2a>-3,求得a>-
| 5 |
| 2 |
综合可得-2≤a<0.
③当-8<a<-2时,二次函数g(t)的图象的对称轴方程为t=-
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
由a+1-
| a2 |
| 4 |
| 5 |
| 5 |
| 5 |
④当a≤-8,二次函数g(t)的图象的对称轴方程为t=-
| a |
| 2 |
g(t)的最小值为g(4)=5a+17,由5a+17>-3,求得a>-4,不满足前提条件a≤-8,故舍去.
综合①②③④可得,a≥2-2
| 5 |
(3)f(x)的零点的个数,即函数g(t)=t2+at+a+1在(0,+∞)上的零点个数.
①当△=a2-4(a+1)<0时,即2-2
| 2 |
| 2 |
②当a=2-2
| 2 |
| 2 |
| a |
| 2 |
可得当a=2-2
| 2 |
| a |
| 2 |
| 2 |
| a |
| 2 |
③当a<2-2
| 2 |
| a |
| 2 |
当a>2+2
| 2 |
| a |
| 2 |
综上可得,a>2-2
| 2 |
当a=2-2
| 2 |
当a<2-2
| 2 |
点评:本题主要考查指数函数的值域,二次函数的性质,函数的恒成立问题,函数零点的个数判断,体现了转化、分类讨论的数学思想,属于难题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
双曲线x2-2y2=1的离心率是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
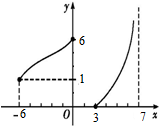 函数y=f(x)的图象如图所示,则函数y=f(x)的定义域为
函数y=f(x)的图象如图所示,则函数y=f(x)的定义域为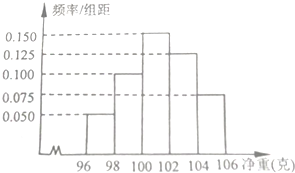 某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了100件产品的净重,所得数据均在区间[96,106]中,其频率分布直方图如图所示,则在抽测的100件产品中,净重在区间[100,104]上的产品件数是
某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了100件产品的净重,所得数据均在区间[96,106]中,其频率分布直方图如图所示,则在抽测的100件产品中,净重在区间[100,104]上的产品件数是