题目内容

双曲线x2-2y2=1的离心率是（　　）
A、
3
2
B、
6
2
C、
3
D、3
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：先将双曲线方程化为标准方程，求得a，b，c，再由离心率公式计算即可得到．
解答： 解：双曲线x2-2y2=1即为x2-
y2
1
2
=1，
即有a2=1，b2=
2
2
，c=
a2+b2
=
1+
1
2
=
6
2
，
则e=
c
a
=
6
2

故答案为：B．
点评：本题考查双曲线的方程和性质，主要考查离心率的求法，属于基础题．
练习册系列答案
相关题目
已知等差数列的前4项之和为21，末4项之和为67，前n项和为286，求n的值．
关于x的不等式x2-ax+1≤0的解集中整数只有1，则a的取值范围是（　　）
A、2≤a＜
5
2
B、2＜a≤
5
2
C、2≤a≤
5
2
D、2＜a＜
5
2
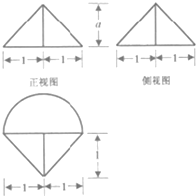一个几何体的三视图如图，其中正视图和侧视图是相同的等腰三角形，俯视图由半圆和一等腰三角形组成．则这个几何体可以看成是由
 
  和
 
组成的，若它的体积是
π+2
6
，则a=
 
．
写出求解二元一次方程组
3x-2y=8
4x+y=7
的一个算法．
双曲线
x2
a2
-
y2
4a2
=1（a＞0）的离心率为（　　）
A、
5
B、
5
2
C、2
D、
3
已知面积为S的凸四边形中，四条边长分别记为a1，a2，a3，a4，点P为四边形内任意一点，且点P到四边的距离分别记为h1，h2，h3，h4，若
a1
1
=
a2
2
=
a3
3
=
a4
4
=k，则h1+2h2+3h3+4h4=
2S
k
类比以上性质，体积为y的三棱锥的每个面的面积分别记为Sl，S2，S3，S4，此三棱锥内任一点Q到每个面的距离分别为H1，H2，H3，H4，若
S1
1
=
S2
2
=
S3
3
=
S4
4
=K，则H1+2H2+3H3+4H4=（　　）
A、
4V
K
B、
3V
K
C、
2V
K
D、
V
K
已知i是虚数单位，若z1=a+
3
2
i，z2=a-
3
2
i，若
z1
z2
为纯虚数，求实数a的值．
若函数f（x）=22x+2xa+a+1．
（1）求函数f（x）的值域；
（2）若f（x）＞-3对任意的x∈[0，2]恒成立，求a的取值范围；
（3）讨论f（x）的零点的个数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网