题目内容
已知数列{an}的前n项和Sn，若an+1-an=2，且a2+a8=a4，则S9= ．
考点：等差数列的前n项和,数列递推式
专题：等差数列与等比数列
分析：根据an+1-an=2，得出{an}是公差为2的等差数列，从而求出a1的值，即得S9的值．
解答：
解：数列{an}中，∵an+1-an=2，
∴{an}是公差为2的等差数列，
又∵a2+a8=a4，
∴（a1+2）+（a1+2×7）=a1+2×3，
解得a1=-10；
∴S9=9×（-10）+
=-18．
故答案为：-18．
∴{an}是公差为2的等差数列，
又∵a2+a8=a4，
∴（a1+2）+（a1+2×7）=a1+2×3，
解得a1=-10；
∴S9=9×（-10）+
| 9×8×2 |
| 2 |
故答案为：-18．
点评：本题考查了等差函数的定义、通项公式以及前n项和公式的应用问题，解题时应熟练地掌握等差数列的有过知识，是基础题．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
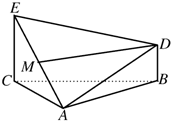如图所示，已知△ABC是等边三角形，EC⊥平面ABC，BD⊥平面ABC，且EC、DB在平面ABC的同侧，M为EA的中点，CE=2BD．