题目内容
18.定义函数F(a,b)=$\frac{1}{2}$(a+b-|a-b|)(a,b∈R),设函数f(x)=-x2+2x+4,g(x)=x+2(x∈R),函数F(f(x),g(x))的最大值与零点之和为6.分析 确定函数F(a,b)=$\frac{1}{2}$(a+b-|a-b|)的含义,表示出G(x)=F(f(x),g(x)),根据一次函数与二次函数的性质可求函数的最大值.
解答 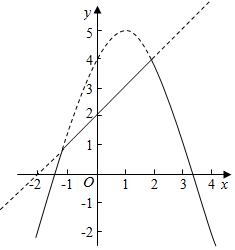 解:∵F(a,b)=$\frac{1}{2}$(a+b-|a-b|)=$\left\{\begin{array}{l}{b,a≥b}\\{a,a<b}\end{array}\right.$,
解:∵F(a,b)=$\frac{1}{2}$(a+b-|a-b|)=$\left\{\begin{array}{l}{b,a≥b}\\{a,a<b}\end{array}\right.$,
∴设G(x)=F(f(x),g(x))=$\left\{\begin{array}{l}{g(x),f(x)≥g(x)}\\{f(x),f(x)<g(x)}\end{array}\right.$.
∵当-1≤x≤2时,f(x)≥g(x),此时G(x)=x+2∈[1,4],此时函数无零点,此时最大值为4
当x>2或x<-1时,f(x)<g(x),G(x)=-x2+2x+4=-(x-1)2+3<4,
综上可得,函数G(x)的最大值为4,
由G(x)=-x2+2x+4=0,得方程的两根之和为2,
则函数F(f(x),g(x))的最大值与零点之和为2+4=6,
故答案为:6.
点评 本题主要考查分段函数的应用,以及函数的最值的求解,解题的关键是根据题目中的定义求出函数G(x)的解析式.利用数形结合是解决本题的关键.

练习册系列答案
相关题目
13.已知正方体ABCD-A1B1C1D1的边长为a,则异面直线AC1与BD的距离为( )
| A. | $\sqrt{3}$a | B. | $\frac{\sqrt{3}}{2}$a | C. | $\frac{\sqrt{6}}{3}$a | D. | $\frac{\sqrt{6}}{6}$a |
8.已知函数f(x)=sinx+λcosx(λ∈R)的图象关于直线x=-$\frac{π}{4}$对称,把函数f(x)的图象上,每个点的横坐标扩大到原来的2倍,纵坐标不变,再将所得函数图象向右平移$\frac{π}{3}$个单位长度,得到函数g(x)的图象,则函数g(x)的一个对称中心是( )
| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{4}$,0) | C. | ($\frac{2π}{3}$,0) | D. | ($\frac{5π}{6}$,0) |