题目内容
6.在数列{an}中,已知a1<$\frac{3}{2}$,an+1=an2-an+1(n∈N*),且$\frac{1}{{a}_{1}}$$+\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2015}}$=2,则当a2016-4a1取得最小值时,a1的值为$\frac{5}{4}$.分析 把已知数列递推式变形,可得$\frac{1}{{a}_{n}}=\frac{1}{{a}_{n}-1}-\frac{1}{{a}_{n+1}-1}$,代入$\frac{1}{{a}_{1}}$$+\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2015}}$=2,整理得到${a}_{2016}=\frac{{a}_{1}-2}{2{a}_{1}-3}$,把a2016-4a1化为含有a1的函数式,然后利用基本不等式求得最值,同时求得a1的值.
解答 解:由an+1=an2-an+1,得an+1-1=an(an-1),可得an>1,
则$\frac{1}{{a}_{n}}=\frac{1}{{a}_{n}-1}-\frac{1}{{a}_{n+1}-1}$.
∴2=$\frac{1}{{a}_{1}}$$+\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2015}}$=($\frac{1}{{a}_{1}-1}-\frac{1}{{a}_{2}-1}$)+($\frac{1}{{a}_{2}-1}-\frac{1}{{a}_{3}-1}$)+…+($\frac{1}{{a}_{2015}-1}-\frac{1}{{a}_{2016}-1}$)
=($\frac{1}{{a}_{1}-1}-\frac{1}{{a}_{2016}-1}$).
化为${a}_{2016}=\frac{{a}_{1}-2}{2{a}_{1}-3}$,
∴a2016-4a1=$\frac{{a}_{1}-2}{2{a}_{1}-3}-4{a}_{1}=\frac{{a}_{1}-2-8{{a}_{1}}^{2}+12{a}_{1}}{2{a}_{1}-3}$
=$\frac{-8{{a}_{1}}^{2}+13{a}_{1}-2}{2{a}_{1}-3}$=$-2(2{a}_{1}-3)-\frac{1}{2(2{a}_{1}-3)}-\frac{11}{2}$.
∵a1<$\frac{3}{2}$,∴2a1-3<0,
则a2016-4a1=$-2(2{a}_{1}-3)-\frac{1}{2(2{a}_{1}-3)}-\frac{11}{2}$
$≥2\sqrt{-2(2{a}_{1}-3)•(-\frac{1}{2(2{a}_{1}-3)})}-\frac{11}{2}$=$2-\frac{11}{2}=-\frac{7}{2}$.
当且仅当$(2{a}_{1}-3)^{2}=\frac{1}{4}$,即$2{a}_{1}-3=-\frac{1}{2}$,也就是${a}_{1}=\frac{5}{4}$时取等号.
故a2016-4a1取得最小值时,a1的值为$\frac{5}{4}$.
故答案为:$\frac{5}{4}$.
点评 本题考查数列递推式,训练了累加法求数列的通项公式,考查了数列的函数特性,是中档题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案| A. | y2=$\frac{16\sqrt{3}}{3}$x | B. | y2=16x | C. | y2=$\frac{8\sqrt{3}}{3}$x | D. | y2=8x |
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$或$\frac{3π}{4}$ | D. | $\frac{π}{3}$ |
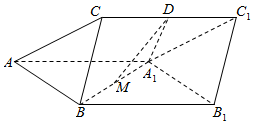 如图,三棱柱ABC-A1B1C1中,D、M分别为CC1和A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,D、M分别为CC1和A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.