题目内容
3.做一个圆柱形锅炉,容积为8π,两个底面的材料每单位面积的价格为2元,侧面的材料每单位面积的价格为4元,当造价最低时,锅炉的底面半径为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 用底面半径r表示出圆柱的高,得出造价关于底面半径r的函数,利用基本不等式或函数单调性求出函数取最小值时的底面半径r.
解答 解:设圆柱形锅炉的底面半径为r,高为h,
则V=πr2h=8π,∴h=$\frac{8}{{r}^{2}}$.
∴锅炉的造价为f(r)=2×2πr2+4×2πrh=4πr2+$\frac{64π}{r}$=4πr2+$\frac{32π}{r}$+$\frac{32π}{r}$≥3$\root{3}{4π{r}^{2}×\frac{32π}{r}×\frac{32π}{r}}$.
当且仅当4πr2=$\frac{32π}{r}$即r=2时取等号.
故选:B.
点评 本题考查了圆柱的体积,基本不等式的应用,求出造价关于半径r的函数是解题关键,属于中档题.

练习册系列答案
相关题目
11.过原点的一条直线与双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)交于A,B两点,P为双曲线上不同于A,B的一个动点,且直线PA、PB的斜率之积为3,若抛物线C2:y2=2px(p>0)的焦点到双曲线C1的渐近线的距离为2,则该抛物线C2的标准方程为( )
| A. | y2=$\frac{16\sqrt{3}}{3}$x | B. | y2=16x | C. | y2=$\frac{8\sqrt{3}}{3}$x | D. | y2=8x |
8.在平面直角坐标系中,过原点O的直线l与曲线y=ex-2交于不同的两点A、B,分别过A、B作x轴的垂线,与曲线y=lnx交于点C、D,则直线CD的斜率为( )
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
12.若函数f(x)=b+lg($\sqrt{{x}^{2}+1}$-ax)是定义在R上的奇函数,则a+b=( )
| A. | -1 | B. | 0 | C. | -1或1 | D. | 0或2 |
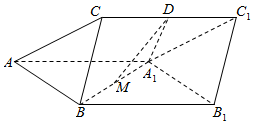 如图,三棱柱ABC-A1B1C1中,D、M分别为CC1和A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,D、M分别为CC1和A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.