题目内容
10.设三角形三边长为3,4,5,P是三角形内的一点,则P到这三角形三边距离乘积的最大值是$\frac{4}{15}$.分析 由勾股定理的逆定理推知该三角形为直角三角形.如图,将△ABC的面积转化为三个三角形的面积之和的形式,根据题意列出不等式,通过解不等式求得答案即可.
解答 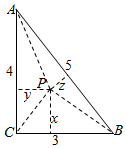 解:如图,∵三角形三边长为3,4,5,
解:如图,∵三角形三边长为3,4,5,
∴32+42=52,
∴△ABC是直角三角形.
设P到长度为3,4,5的三角形三边的距离分别是 x,y,z,三角形的面积为S.
则S=$\frac{1}{2}$(3x+4y+5z)=$\frac{1}{2}$×3×4,即3x+4y+5z=12,
∵12=3x+4y+5z≥3×$\sqrt{3x×4y×5z}$,即2≥$\sqrt{15xyz}$,(当且仅当3x=4y=5z时等号成立),
∴xyz≤$\frac{4}{15}$.
∴P到这三角形三边距离乘积的最大值是$\frac{4}{15}$.
点评 本题考查了点到直线的距离,基本不等式以及三角形的面积.解题的关键是建立数学模型,利用基本不等式的知识求得P到这三角形三边距离乘积的最大值.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
20.已知双曲线C:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线与直线y=-1所围成的三角形的面积为4,则双曲线C的离心率为( )
| A. | $\sqrt{15}$ | B. | $\frac{\sqrt{17}}{2}$ | C. | $\sqrt{17}$ | D. | $\frac{\sqrt{15}}{2}$ |
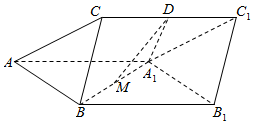 如图,三棱柱ABC-A1B1C1中,D、M分别为CC1和A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,D、M分别为CC1和A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.