题目内容
7.判断y=sinx+tanx的奇偶性.分析 求出函数的定义域,判断是否关于原点对称,在计算f(-x),判断与f(x)的关系,得出结论.
解答 解:令f(x)=sinx+tanx,
则f(x)的定义域为{x|x≠$\frac{π}{2}$+kπ,k∈Z},关于原点对称.
f(-x)=sin(-x)+tan(-x)=-sinx-tanx=-f(x).
∴y=sinx+tanx是奇函数.
点评 本题考查了函数奇偶性的判断,属于基础题.

练习册系列答案
相关题目
12.若函数f(x)=b+lg($\sqrt{{x}^{2}+1}$-ax)是定义在R上的奇函数,则a+b=( )
| A. | -1 | B. | 0 | C. | -1或1 | D. | 0或2 |
16.若sinα=$\frac{1}{\sqrt{5}}$,sinβ=$\frac{1}{\sqrt{10}}$,且α、β∈(0,$\frac{π}{2}$),则α+β是( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$或$\frac{3π}{4}$ | D. | $\frac{π}{3}$ |
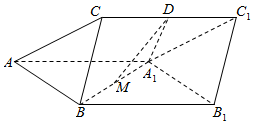 如图,三棱柱ABC-A1B1C1中,D、M分别为CC1和A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,D、M分别为CC1和A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.