题目内容
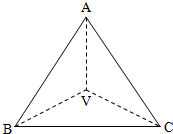 如图,已知VA,VB,VC两两垂直,VA=VB=VC=a.
如图,已知VA,VB,VC两两垂直,VA=VB=VC=a.(1)求平面ABC和平面ABV所成的二面角的余弦值;
(2)求三棱锥V-ABC的体积.
考点:棱柱、棱锥、棱台的体积,与二面角有关的立体几何综合题
专题:计算题,空间位置关系与距离,空间角
分析:(1)求出S△ABV=
a2,S△ABC=
a2,即可求出平面ABC和平面ABV所成的二面角的余弦值;
(2)利用VA,VB,VC两两垂直,VA=VB=VC=a,根据体积公式,容易得出结论.
| 1 |
| 2 |
| ||
| 2 |
(2)利用VA,VB,VC两两垂直,VA=VB=VC=a,根据体积公式,容易得出结论.
解答:
解:(1)∵VA,VB,VC两两垂直,VA=VB=VC=a,
∴AB=BC=AC=
a,
∴S△ABV=
a2,S△ABC=
a2,
∴平面ABC和平面ABV所成的二面角的余弦值为
=
;
(2)三棱锥V-ABC的体积为
•
•a•a•a=
a3.
∴AB=BC=AC=
| 2 |
∴S△ABV=
| 1 |
| 2 |
| ||
| 2 |
∴平面ABC和平面ABV所成的二面角的余弦值为
| ||||
|
| ||
| 3 |
(2)三棱锥V-ABC的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查二面角的平面角,考查学生的计算能力,比较基础.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
设
与
都是单位向量,则下列各式中成立的是( )
| a |
| b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、|
|
-401是等差数列-5,-9,-13…的第( )项.
| A、98 | B、99 |
| C、100 | D、101 |
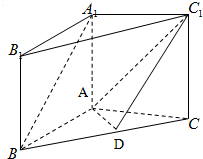 在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2
在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2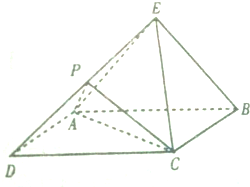 如图,设四棱锥E-ABCD的底面为菱形,且∠ABC=60°,P为DE上一点 若BE∥平面PAC.
如图,设四棱锥E-ABCD的底面为菱形,且∠ABC=60°,P为DE上一点 若BE∥平面PAC.