题目内容
已知a>0,函数f(x)=
+2a,g(x)=alnx-x+a.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)求证:对于任意的x1,x2∈(0,e),都有f(x1)>g(x2).
| ax |
| x2+1 |
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)求证:对于任意的x1,x2∈(0,e),都有f(x1)>g(x2).
考点:利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)求出函数的定义域、导数,在定义域内解不等式f′(x)<0,f′(x)>0即可得到函数的单调区间;
(Ⅱ)只需证明f(x)min>g(x)max,利用导数可求得f(x)min;分a≥e、0<a<e两种情况进行讨论,利用导数可求得g(x)max;
(Ⅱ)只需证明f(x)min>g(x)max,利用导数可求得f(x)min;分a≥e、0<a<e两种情况进行讨论,利用导数可求得g(x)max;
解答:
(Ⅰ)解:函数f(x)的定义域为R,f′(x)=
=
,
∵a>0,
∴当x<-1,或x>1时,f′(x)<0;当-1<x<1时,f′(x)>0.
∴f(x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞).
(Ⅱ)证明:f(x)在区间(0,1)上单调递增,在区间(1,e)上单调递减,
又f(0)=2a,f(e)=
+2a>2a,
∴当x∈(0,e)时,f(x)>2a.
由g(x)=alnx-x+a,可得g′(x)=
-1=
.
∴当a≥e时,函数g(x)在区间(0,e)上是增函数,
∴当x∈(0,e)时,g(x)<g(e)=2a-e<2a.
∴当x∈(0,e)时,
对于任意的x1,x2∈(0,e),都有f(x1)>2a,g(x2)<2a,∴f(x1)>g(x2).
当0<a<e时,函数g(x)在区间(0,a)上是增函数,在区间(a,e)上是减函数,
∴当x∈(0,e)时,g(x)≤g(a)=alna<2a.
∴当x∈(0,e)时,
对于任意的x1,x2∈(0,e),都有f(x1)>2a,g(x2)<2a,所以f(x1)>g(x2).
综上,对于任意的x1,x2∈(0,e),都有f(x1)>g(x2). …(13分)
| a(1-x2) |
| (x2+1)2 |
| a(1-x)(1+x) |
| (x2+1)2 |
∵a>0,
∴当x<-1,或x>1时,f′(x)<0;当-1<x<1时,f′(x)>0.
∴f(x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞).
(Ⅱ)证明:f(x)在区间(0,1)上单调递增,在区间(1,e)上单调递减,
又f(0)=2a,f(e)=
| ea |
| e2+1 |
∴当x∈(0,e)时,f(x)>2a.
由g(x)=alnx-x+a,可得g′(x)=
| a |
| x |
| a-x |
| x |
∴当a≥e时,函数g(x)在区间(0,e)上是增函数,
∴当x∈(0,e)时,g(x)<g(e)=2a-e<2a.
∴当x∈(0,e)时,
对于任意的x1,x2∈(0,e),都有f(x1)>2a,g(x2)<2a,∴f(x1)>g(x2).
当0<a<e时,函数g(x)在区间(0,a)上是增函数,在区间(a,e)上是减函数,
∴当x∈(0,e)时,g(x)≤g(a)=alna<2a.
∴当x∈(0,e)时,
对于任意的x1,x2∈(0,e),都有f(x1)>2a,g(x2)<2a,所以f(x1)>g(x2).
综上,对于任意的x1,x2∈(0,e),都有f(x1)>g(x2). …(13分)
点评:该题考查利用导数研究函数的单调性、最值,考查函数恒成立问题,考查转化思想,考查学生分析解决问题的能力.

练习册系列答案
相关题目
△ABC中,如果
=
=
,那么△ABC是( )
| a |
| tanA |
| b |
| tanB |
| c |
| tanC |
| A、直角三角形 |
| B、等边三角形 |
| C、等腰直角三角形 |
| D、钝角三角形 |
设集合A={-2,0,3,4},B={x|x2-2x-3=0},则A∩B=( )
| A、{0} | B、{3} |
| C、{0,2} | D、{0,2,4} |
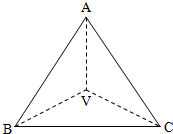 如图,已知VA,VB,VC两两垂直,VA=VB=VC=a.
如图,已知VA,VB,VC两两垂直,VA=VB=VC=a.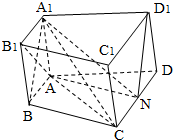 如图,在侧棱与底面垂直的四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥BC,且A1A=AB=BC=1,CD=2.
如图,在侧棱与底面垂直的四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥BC,且A1A=AB=BC=1,CD=2.